
رگرسیون خطی
رگرسیون خطی روابط بین حداقل یک متغیر توضیحی و یک متغیر نتیجه را مدلسازی میکند. این تحلیل انعطافپذیر به شما امکان میدهد تا اثرات سوالات پیچیده تحقیق را از هم جدا کنید و نقش هر متغیر را جداگانه بررسی کنید. علاوه بر این، مدلهای خطی میتوانند اثرات انحنا و تعامل را برازش دهند.
آمارشناسان به متغیرهای توضیحی در رگرسیون خطی به عنوان متغیرهای مستقل (IV) و به نتیجه به عنوان متغیرهای وابسته (DV) اشاره میکنند. وقتی یک مدل خطی یک IV دارد، این روش به عنوان رگرسیون خطی ساده شناخته میشود. وقتی بیش از یک IV وجود دارد، آمارشناسان به آن رگرسیون چندگانه میگویند. این مدلها فرض میکنند که مقدار متوسط متغیر وابسته به یک تابع خطی از متغیرهای مستقل بستگی دارد.
اهداف رگرسیون خطی
رگرسیون خطی دو هدف اصلی دارد – درک روابط بین متغیرها و پیشبینی.
ضرایب نشاندهنده بزرگی و جهت تخمینی (مثبت/منفی) رابطه بین هر متغیر مستقل و متغیر وابسته هستند.
این معادله به شما امکان میدهد مقدار متوسط متغیر وابسته را با توجه به مقادیر متغیرهای مستقلی که مشخص میکنید، پیشبینی کنید.
رگرسیون خطی، مقادیر ثابت و ضریب را برای متغیرهای مستقل خطی که به بهترین وجه با دادههای نمونه شما مطابقت دارند، پیدا میکند. نمودار زیر بهترین برازش خطی را برای نقاط داده قد و وزن نشان میدهد و رابطه ریاضی بین آنها را آشکار میکند. ضریب قد، شیب خط است. علاوه بر این، میتوانید از معادله خط برای پیشبینی مقادیر آینده وزن با توجه به قد یک فرد استفاده کنید.
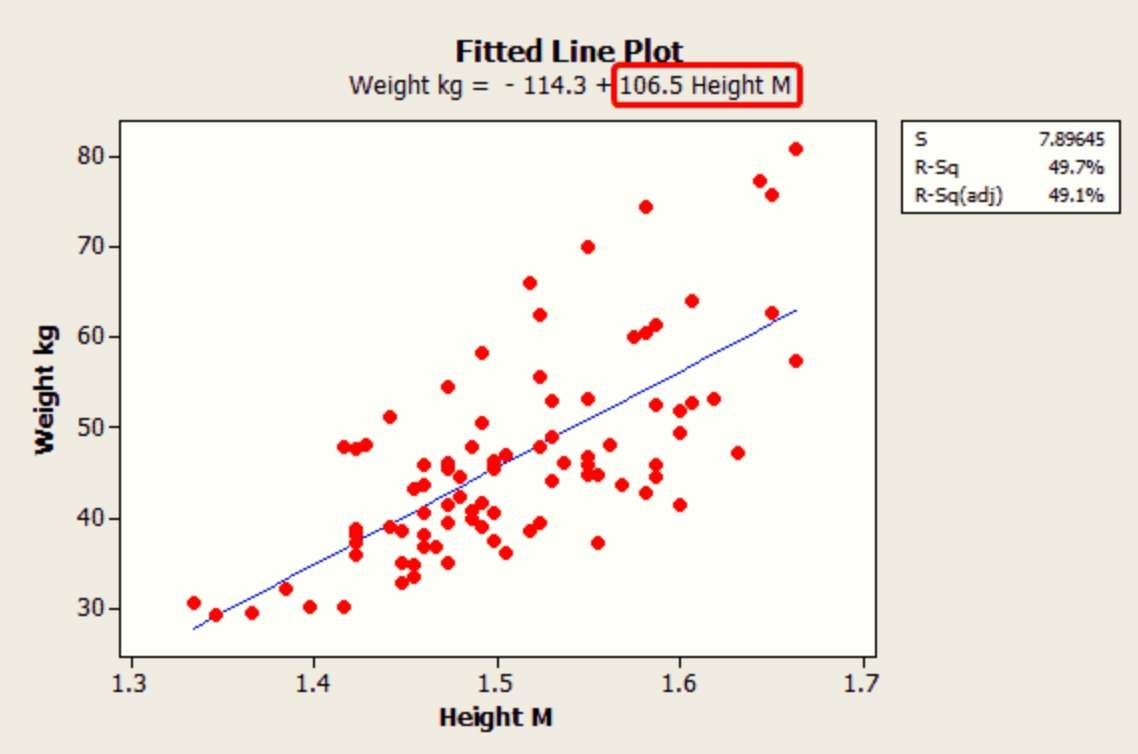
رگرسیون خطی یکی از اولین انواع تحلیل رگرسیون بود که به طور دقیق مورد مطالعه قرار گرفت و به طور گسترده در سناریوهای دنیای واقعی به کار گرفته شد. این محبوبیت ناشی از سهولت نسبی برازش مدلهای خطی به دادهها و ماهیت سرراست تحلیل ویژگیهای آماری این مدلها است. برخلاف مدلهای پیچیدهتر که به روشی غیرخطی به پارامترهای خود مربوط میشوند، مدلهای خطی هم تخمین و هم تفسیر دادهها را ساده میکنند.
در این پست، نحوه تفسیر رگرسیون خطی را با یک مثال، در مورد فرمول خطی، نحوه یافتن تخمین ضرایب و فرضیات آن خواهید آموخت.
مثال رگرسیون خطی
فرض کنید از رگرسیون خطی برای مدلسازی چگونگی ارتباط دمای بیرون بر حسب سانتیگراد و ضخامت عایق بر حسب سانتیمتر، دو متغیر مستقل ما، با هزینههای تهویه مطبوع بر حسب دلار (متغیر وابسته) استفاده میکنیم.
بیایید نتایج معادله رگرسیون خطی چندگانه زیر را تفسیر کنیم:
هزینههای تهویه مطبوع ($) = 2 * دما (C) – 1.5 * عایق (CM)
علامت ضریب دما مثبت (+2) است که نشان دهنده رابطه مثبت بین دما و هزینهها است. با افزایش دما، هزینههای تهویه مطبوع نیز افزایش مییابد. به طور خاص، مقدار ضریب 2 نشان میدهد که به ازای هر 1 درجه سانتیگراد افزایش، میانگین هزینه تهویه مطبوع دو دلار افزایش مییابد.
از سوی دیگر، ضریب منفی عایق (-1.5) نشان دهنده رابطه منفی بین عایق و هزینههای تهویه مطبوع است. با افزایش ضخامت عایق، هزینههای تهویه مطبوع کاهش مییابد. به ازای هر 1 سانتیمتر افزایش، میانگین هزینه تهویه مطبوع 1.50 دلار کاهش مییابد.
همچنین میتوانیم مقادیر دما و عایق را در این معادله رگرسیون خطی وارد کنیم تا میانگین هزینه تهویه مطبوع را پیشبینی کنیم.
فرمول رگرسیون خطی
این نوع رگرسیون به شکل معادلات رگرسیونی که این مدلها استفاده میکنند اشاره دارد. این مدلها از یک فرمول خاص پیروی میکنند که مستلزم آن است که همه عبارات یکی از موارد زیر باشند:
ثابت
پارامتری ضرب شده در یک متغیر مستقل (IV)
سپس، فرمول رگرسیون خطی را با جمع کردن عبارات با هم میسازید. این قوانین، فرم را فقط به یک نوع محدود میکنند:
متغیر وابسته = ثابت + پارامتر * IV + … + پارامتر * IV
این فرمول در پارامترها خطی است. با این حال، علیرغم نام رگرسیون خطی، میتواند انحنا را مدلسازی کند. در حالی که فرمول باید در پارامترها خطی باشد، میتوانید یک متغیر مستقل را با توانی افزایش دهید تا انحنا را مدلسازی کند. به عنوان مثال، اگر یک متغیر مستقل را به توان دو برسانید، رگرسیون خطی میتواند یک منحنی U شکل را برازش دهد.
تعیین مدل خطی صحیح نیاز به ایجاد تعادل بین دانش موضوعی، نتایج آماری و برآورده کردن فرضیات دارد.
نحوه یافتن خط رگرسیون خطی
رگرسیون خطی میتواند از روشهای تخمین مختلفی برای یافتن بهترین خط برازش استفاده کند. با این حال، تحلیلگران بیشتر از روش حداقل مربعات استفاده میکنند زیرا دقیقترین روش پیشبینی است که به طور سیستماتیک مقادیر صحیح را بیش از حد یا کمتر از حد تخمین نمیزند، زمانی که بتوانید تمام فرضیات آن را برآورده کنید.
زیبایی روش حداقل مربعات، سادگی و کارایی آن است. محاسبات مورد نیاز برای یافتن بهترین خط برازش ساده است، که آن را حتی برای مبتدیان قابل دسترسی میکند و به طور گسترده در کاربردهای آماری مختلف استفاده میشود. در اینجا نحوه کار آن آمده است:
هدف: به حداقل رساندن تفاوتهای بین مقادیر مشاهده شده و پیشبینی شده مدل رگرسیون خطی. این تفاوتها به عنوان “باقیماندهها” شناخته میشوند و نشان دهنده خطاهای موجود در مقادیر مدل هستند.
به حداقل رساندن خطاها: این روش بر کوچک کردن مجموع این مربعات تفاوتها تا حد امکان تمرکز دارد.
خط بهترین برازش: با یافتن مقادیر پارامترهای مدل که به این حداقل مجموع میرسند، روش حداقل مربعات به طور موثر بهترین خط برازش را از طریق نقاط داده تعیین میکند.
با استفاده از روش حداقل مربعات در رگرسیون خطی و بررسی فرضیات در بخش بعدی، میتوانید اطمینان حاصل کنید که مدل شما تا حد امکان دقیق و بیطرف است. توانایی این روش در به حداقل رساندن خطاها و یافتن بهترین خط برازش، یک دارایی ارزشمند در تحلیل آماری است.
مفروضات
رگرسیون خطی با استفاده از روش حداقل مربعات دارای فرضیات زیر است:
یک مدل خطی به طور رضایتبخشی با رابطه برازش دارد.
باقیماندهها از توزیع نرمال پیروی میکنند.
باقیماندهها پراکندگی ثابتی دارند.
مشاهدات مستقل.
IVها کاملاً همبسته نیستند.
باقیماندهها تفاوت بین مقدار مشاهده شده و مقدار میانگینی هستند که مدل برای آن مشاهده پیشبینی میکند. اگر فرضیات را برآورده نکنید، نتایج ممکن است معتبر نباشند.




پاسخگوی سوالات و نظرات شما هستیم