اثر متقابل یا اثر تعاملی

اثرات متقابل چیست؟

اثر متقابل زمانی رخ می‌دهد که اثر یک متغیر به مقدار متغیر دیگری بستگی داشته باشد. اثرات متقابل در مدل‌های رگرسیون، آنالیز واریانس (ANOVA) و آزمایش‌های طراحی‌شده رایج هستند. در این پست، اثرات متقابل، آزمون اثر متقابل، نحوه تفسیر مدل‌های تعامل و مشکلاتی را که در صورت عدم لحاظ کردن آنها در مدل خود با آنها مواجه می‌شوید، توضیح می‌دهم.

در هر مطالعه‌ای، چه یک آزمون چشایی باشد و چه یک فرآیند تولید، متغیرهای زیادی می‌توانند بر نتیجه تأثیر بگذارند. تغییر این متغیرها می‌تواند مستقیماً بر نتیجه تأثیر بگذارد. به عنوان مثال، تغییر چاشنی غذا در یک آزمون چشایی می‌تواند بر لذت کلی تأثیر بگذارد. به این ترتیب، تحلیلگران از مدل‌ها برای ارزیابی رابطه بین هر متغیر مستقل و متغیر وابسته استفاده می‌کنند. این نوع اثر، اثر اصلی نامیده می‌شود. در حالی که اثرات اصلی نسبتاً ساده هستند، ارزیابی فقط اثرات اصلی می‌تواند اشتباه باشد.

در حوزه‌های مطالعاتی پیچیده‌تر، متغیرهای مستقل ممکن است با یکدیگر تعامل داشته باشند. اثرات متقابل نشان می‌دهد که یک متغیر سوم بر رابطه بین یک متغیر مستقل و وابسته تأثیر می‌گذارد. در این شرایط، آماردانان می‌گویند که این متغیرها با هم تعامل دارند زیرا رابطه بین یک متغیر مستقل و وابسته بسته به مقدار یک متغیر سوم تغییر می‌کند. این نوع اثر، مدل را پیچیده‌تر می‌کند، اما اگر دنیای واقعی به این شکل رفتار می‌کند، گنجاندن آن در مدل شما بسیار مهم است. به عنوان مثال، رابطه بین چاشنی‌ها و لذت بردن احتمالاً به نوع غذا بستگی دارد – همانطور که در این پست خواهیم دید!

در زمینه‌هایی مانند روانشناسی، علوم اجتماعی و تحقیقات بازاریابی، اثرات متقابل اغلب به عنوان اثرات تعدیلی شناخته می‌شوند. محققان در این زمینه‌ها معمولاً به این موضوع علاقه‌مند هستند که چگونه یک متغیر، قدرت یا جهت رابطه بین متغیر مستقل دیگر و نتیجه را تغییر می‌دهد یا تعدیل می‌کند.

مثال اثرات متقابل با متغیرهای مستقل طبقه‌بندی‌شده

ما اثرات متقابل را به عنوان یک اثر «بستگی دارد» در نظر می‌گیریم. خواهید دید که چرا! بیایید با یک مثال شهودی شروع کنیم تا به شما در درک مفهومی این اثرات در یک مدل تعاملی کمک کنیم.

تصور کنید که ما در حال انجام یک آزمایش چشایی هستیم تا مشخص کنیم کدام چاشنی غذا بیشترین لذت را ایجاد می‌کند. ما یک آنالیز واریانس دوطرفه انجام خواهیم داد که در آن متغیر وابسته ما لذت است. دو متغیر مستقل ما هر دو متغیرهای طبقه‌بندی‌شده هستند: غذا و چاشنی.

مدل ANOVA ما با عبارت تعاملی به صورت زیر است:

رضایت = غذا، چاشنی، غذا*چاشنی

برای ساده نگه داشتن مسائل، ما فقط دو غذا (بستنی و هات داگ) و دو چاشنی (سس شکلات و خردل) را در تحلیل خود لحاظ خواهیم کرد.

با توجه به جزئیات مثال، وجود اثر متقابل تعجب‌آور نخواهد بود. اگر کسی از شما بپرسد: «آیا سس کچاپ را برای غذایتان ترجیح می‌دهید یا سس شکلات؟» بدون شک، پاسخ خواهید داد: «بستگی به نوع غذا دارد!» این ماهیت «بستگی دارد» یک اثر متقابل است. شما نمی‌توانید بدون دانستن اطلاعات بیشتر در مورد متغیر دیگر در عبارت متقابل – که نوع غذا در مثال ماست – به این سوال پاسخ دهید!

این مفهوم است. اکنون، به شما نشان خواهیم داد که چگونه یک عبارت متقابل را در مدل خود بگنجانید و چگونه نتایج را تفسیر کنید.

چگونه اثرات متقابل را تفسیر کنیم؟

بستنی با سس شکلاتی برای نشان دادن اثرات متقابل. بیایید تجزیه و تحلیل خود را انجام دهیم. همه نرم‌افزارهای آماری به شما امکان می‌دهند عبارات متقابل را در یک مدل اضافه کنید.

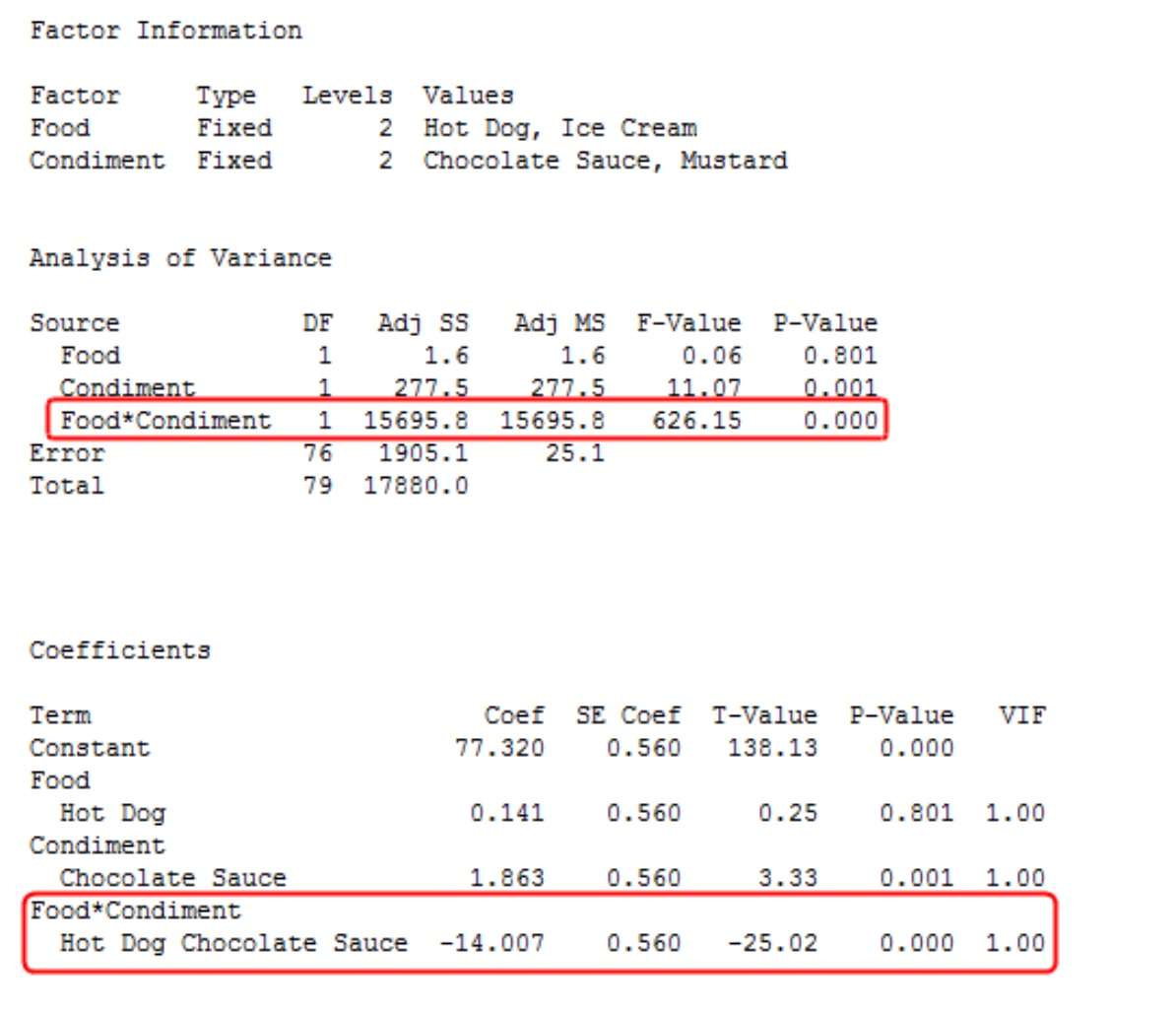
از مقدار p برای یک عبارت تعاملی برای آزمایش معناداری آن استفاده کنید. در خروجی زیر، مقدار p دایره شده به ما می‌گوید که آزمون اثر تعاملی (غذا*ادویه) از نظر آماری معنادار است. در نتیجه، می‌دانیم که رضایت شما از چاشنی به نوع غذا بستگی دارد.

اما چگونه می‌توانیم تعامل را در یک مدل تفسیر کنیم و واقعاً بفهمیم که داده‌ها چه می‌گویند؟ بهترین راه برای درک این اثرات، استفاده از نوع خاصی از نمودار خطی است – نمودار تعامل. این نوع نمودار، مقادیر برازش شده متغیر وابسته را روی محور y نشان می‌دهد در حالی که محور x مقادیر متغیر مستقل اول را نشان می‌دهد. در همین حال، خطوط مختلف، مقادیر متغیر مستقل دوم را نشان می‌دهند.

در یک نمودار تعامل، خطوط موازی نشان می‌دهند که هیچ اثر تعاملی وجود ندارد در حالی که شیب‌های مختلف نشان می‌دهند که ممکن است اثری وجود داشته باشد. در زیر نمودار مربوط به Food*Condiment آمده است.

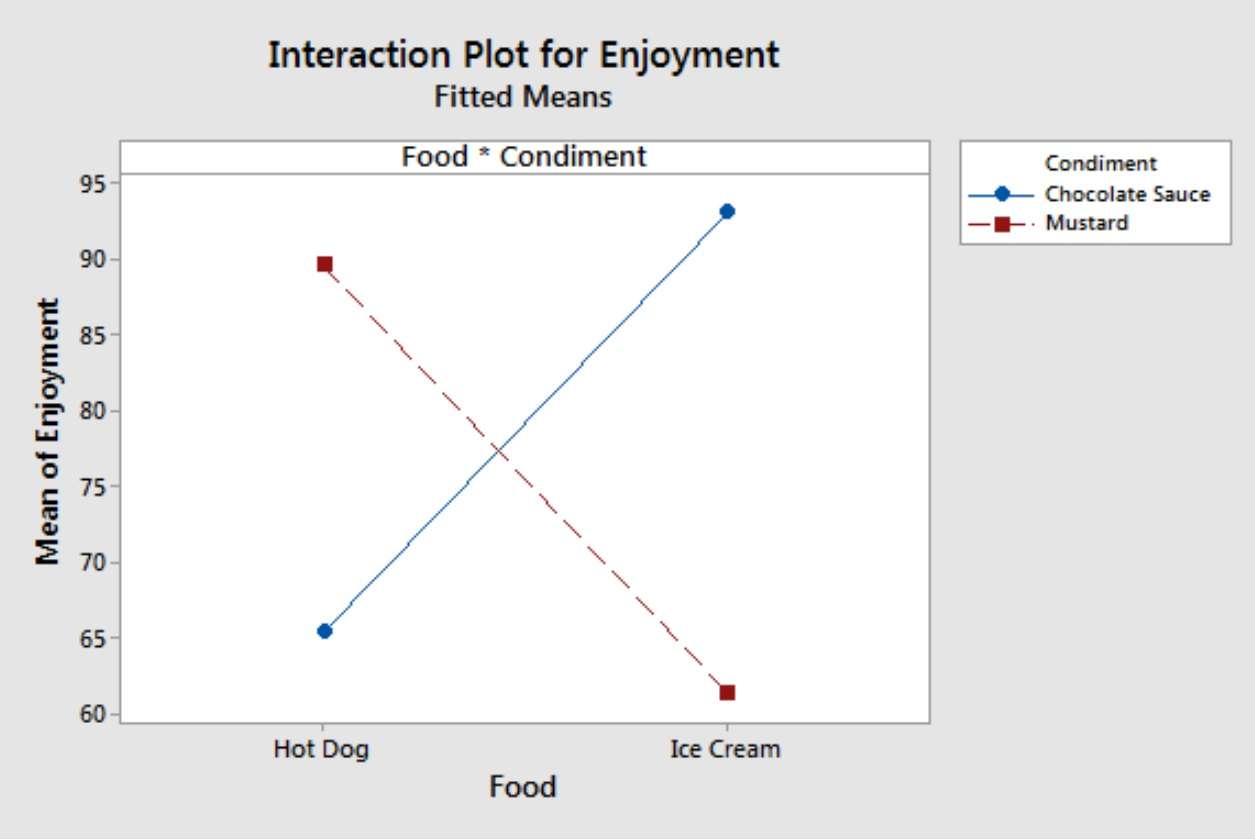
خطوط ضربدری روی نمودار نشان می‌دهند که یک اثر متقابل وجود دارد، که مقدار p-value معنی‌دار برای عبارت Food*Condiment آن را تأیید می‌کند. نمودار نشان می‌دهد که وقتی غذا بستنی است، سطح لذت برای سس شکلات بالاتر است. برعکس، وقتی غذا هات داگ است، سطح رضایت برای سس خردل بالاتر است. اگر خردل را روی بستنی یا سس شکلات روی هات داگ بریزید، خوشحال نخواهید شد!

کدام چاشنی بهتر است؟ بستگی به نوع غذا دارد و ما از آمار برای نشان دادن این اثر استفاده کرده‌ایم.

چشم‌پوشی از اثرات متقابل خطرناک است!

وقتی اثرات متقابل از نظر آماری معنی‌دار هستند، نمی‌توانید اثرات اصلی را بدون در نظر گرفتن اثرات متقابل تفسیر کنید. در مثال قبلی، نمی‌توانید بدون دانستن نوع غذا به این سوال که کدام چاشنی بهتر است پاسخ دهید. باز هم، “بستگی دارد.”

فرض کنید می‌خواهیم با انتخاب بهترین غذا و بهترین چاشنی، رضایت را به حداکثر برسانیم. با این حال، تصور کنید که فراموش کرده‌ایم اثر متقابل را لحاظ کنیم و فقط اثرات اصلی را ارزیابی کرده‌ایم. ما بر اساس نمودارهای اثرات اصلی زیر تصمیم خواهیم گرفت.

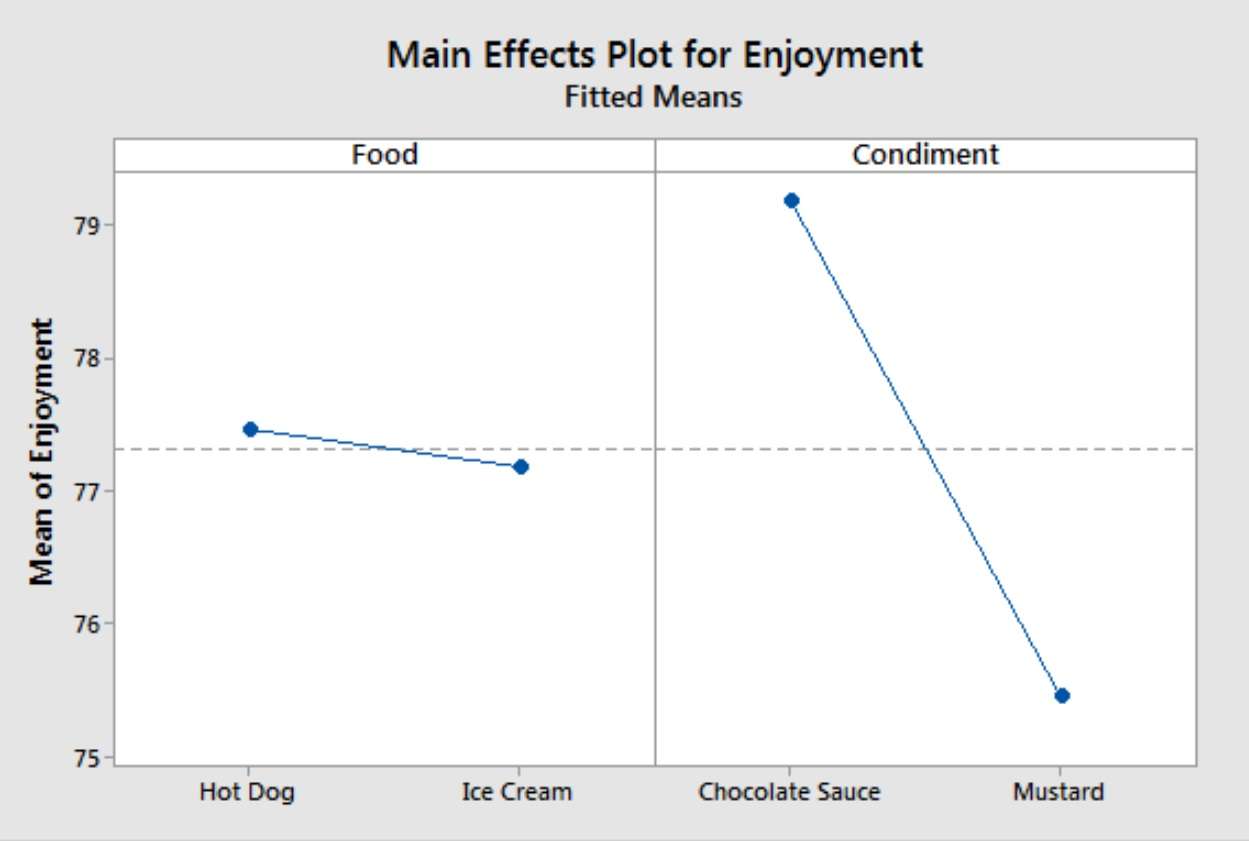
بر اساس این نمودارها، ما هات داگ با سس شکلات را انتخاب می‌کنیم زیرا هر کدام لذت بیشتری ایجاد می‌کنند. این انتخاب خوبی نیست، علیرغم آنچه اثرات اصلی نشان می‌دهند! وقتی تعاملات آماری معناداری دارید، نمی‌توانید اثر اصلی را بدون در نظر گرفتن اثرات متقابل تفسیر کنید.

با توجه به ماهیت عمدی شهودی مثال ساختگی ما، پیامد نادیده گرفتن اثر متقابل در یک نگاه گذرا آشکار است. با این حال، همانطور که در مثال بعدی خواهید دید، همیشه اینطور نیست.

مثالی از اثر متقابل با متغیرهای مستقل پیوسته

برای مثال بعدی، متغیرهای مستقل پیوسته را در یک مدل رگرسیون برای یک فرآیند تولید ارزیابی خواهیم کرد. متغیرهای مستقل (زمان پردازش، دما و فشار) بر متغیر وابسته (قدرت محصول) تأثیر می‌گذارند.

در مدل تعامل، دما*فشار را به عنوان یک اثر متقابل لحاظ خواهم کرد. نتایج در زیر آمده است.

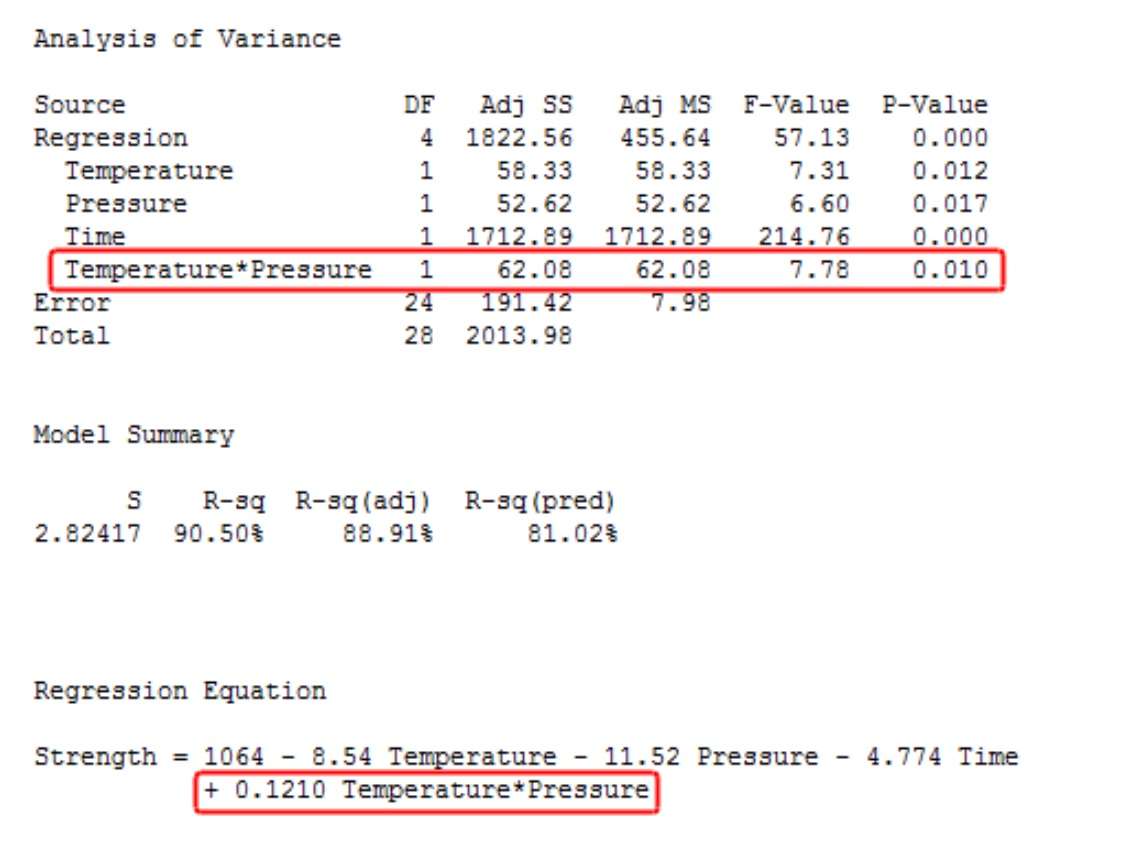
همانطور که می‌بینید، آزمون اثر متقابل از نظر آماری معنادار است. اما چگونه ضریب تعامل را در معادله رگرسیون تفسیر می‌کنید؟ می‌توانید مقادیری را در معادله رگرسیون وارد کنید و مسائل را کنار هم قرار دهید. با این حال، استفاده از نمودارهای تعامل بسیار آسان‌تر است!

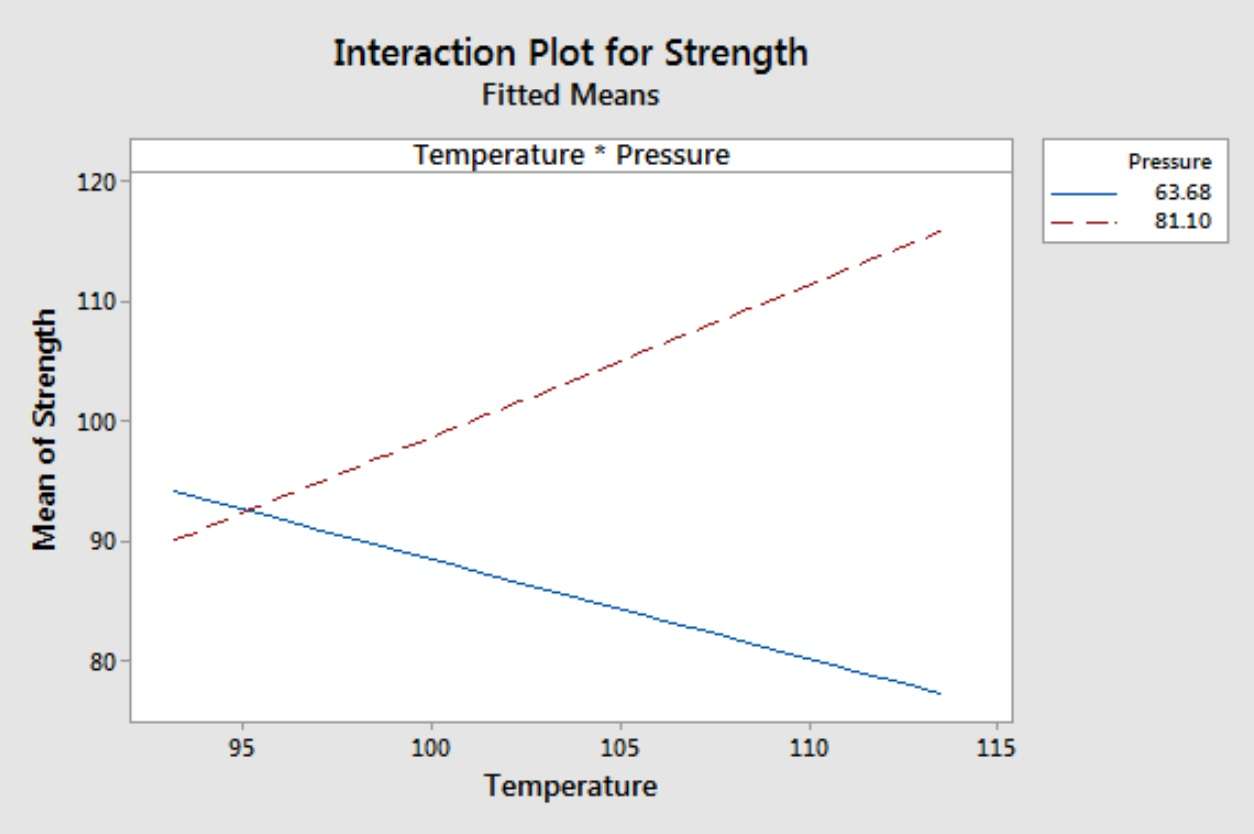
در نمودار بالا، متغیرها پیوسته هستند و نه دسته‌بندی‌شده. برای تولید نمودار، نرم‌افزار آماری یک مقدار بالا و یک مقدار پایین برای فشار انتخاب می‌کند و آنها را به همراه محدوده مقادیر دما وارد معادله می‌کند.

همانطور که می‌بینید، رابطه بین دما و استحکام بر اساس فشار تغییر جهت می‌دهد. برای فشارهای بالا، رابطه مثبتی بین دما و استحکام وجود دارد در حالی که برای فشارهای پایین، رابطه منفی است. با گنجاندن عبارت تعامل در مدل، می‌توانید روابطی را که بر اساس مقدار متغیر دیگری تغییر می‌کنند، ثبت کنید.

اگر می‌خواهید استحکام محصول را به حداکثر برسانید و کسی از شما بپرسد که آیا فرآیند باید از دمای بالا یا پایین استفاده کند، باید پاسخ دهید: “بستگی دارد.” در این مورد، به فشار بستگی دارد. شما نمی‌توانید بدون دانستن مقدار فشار به سوال مربوط به دما پاسخ دهید.

ملاحظات مهم برای اثرات تعاملی

در حالی که نمودارها به شما در تفسیر اثرات تعاملی کمک می‌کنند، از یک آزمون فرضیه برای تعیین اینکه آیا اثر از نظر آماری معنادار است یا خیر، استفاده کنید. نمودارها می‌توانند خطوط غیرموازی را نشان دهند که به جای یک اثر واقعی، خطای نمونه‌گیری تصادفی را نشان می‌دهند. مقادیر P و آزمون‌های فرضیه به شما کمک می‌کنند تا اثرات واقعی را از نویز جدا کنید.

مثال‌های این پست، تعاملات دوطرفه هستند زیرا در هر عبارت دو متغیر مستقل وجود دارد (غذا*چاشنی و دما*فشار). تفسیر این اثرات به دو روش به یک اندازه معتبر است. به عنوان مثال، رابطه بین:

• رضایت و چاشنی به غذا بستگی دارد.
• رضایت و غذا به چاشنی بستگی دارد.

شما می‌توانید تعاملات مرتبه بالاتر داشته باشید. به عنوان مثال، یک تعامل سه‌طرفه دارای سه متغیر در عبارت است، مانند غذا*چاشنی*X. در این مورد، رابطه بین رضایت و چاشنی به غذا و X بستگی دارد. با این حال، تفسیر این نوع اثر چالش برانگیز است. در عمل، تحلیلگران به ندرت از آنها استفاده می‌کنند. با این حال، در برخی مدل‌ها، ممکن است برای ارائه برازش کافی، لازم باشند.

در نهایت، وقتی یک آزمون اثر متقابل از نظر آماری معنادار است، سعی نکنید اثرات اصلی را بدون در نظر گرفتن اثرات متقابل تفسیر کنید. همانطور که مثال‌ها نشان می‌دهند، نتیجه‌گیری‌های اشتباهی خواهید داشت!

مطالب مرتبط مفید

آنالیز واریانس (ANOVA)

تحلیل رگرسیون

مقدار احتمال (p-value) و سطح معناداری