آزمون فرضیه آماری: کاربردها، مراحل و مثالها
آزمون فرضیه چیست؟
آزمون فرضیه در آمار از دادههای نمونه برای استنباط ویژگیهای کل جمعیت استفاده میکند. این آزمونها تعیین میکنند که آیا یک نمونه تصادفی شواهد کافی برای نتیجهگیری در مورد وجود یک اثر یا رابطه در جمعیت را ارائه میدهد یا خیر. محققان از آنها برای کمک به جداسازی اثرات واقعی در سطح جمعیت از اثرات کاذبی که شانس تصادفی میتواند در نمونهها ایجاد کند، استفاده میکنند. این روشها همچنین به عنوان آزمون معناداری شناخته میشوند.
آزمونهای فرضیه، ابزارهای حیاتی تحلیل آماری هستند که اعتبار نظریههای جدید را با مقایسه آنها با دادههای تجربی ارزیابی میکنند. آنها رویکردی ساختارمند برای تصمیمگیری ارائه میدهند و بر بینشهای مبتنی بر داده به جای تعصبات شخصی یا نظرات ذهنی تأکید میکنند. این روش به محققان اجازه میدهد تا تعیین کنند که آیا دادههای آنها از فرضیههایشان پشتیبانی میکند یا خیر و به جلوگیری از ادعاها و نتیجهگیریهای نادرست کمک میکند.
به عنوان مثال، محققان در حال آزمایش یک داروی جدید هستند تا ببینند آیا فشار خون را کاهش میدهد یا خیر. آنها گروهی را که این دارو را مصرف میکنند با گروه کنترلی که دارونما مصرف میکنند مقایسه میکنند. اگر نتایج آزمون فرضیه آنها از نظر آماری معنیدار باشد، احتمالاً اثر دارو در کاهش فشار خون در جمعیت وسیعتر، نه فقط نمونه مورد مطالعه، وجود دارد.
استفاده از آزمونهای فرضیه
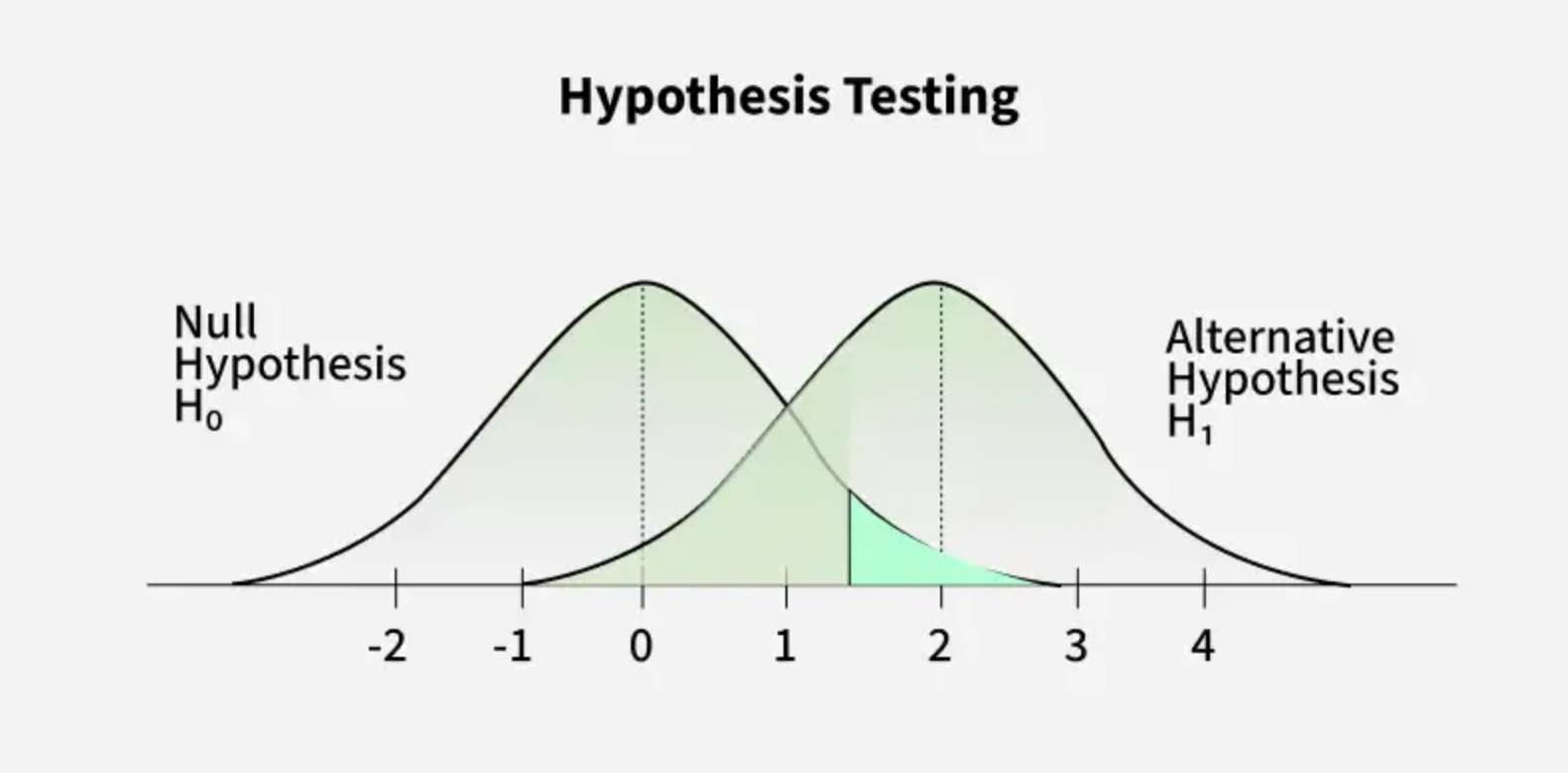
آزمون فرضیه، دو گزاره ناسازگار متقابل در مورد یک جمعیت را ارزیابی میکند تا مشخص شود که دادههای نمونه کدام گزاره را به بهترین وجه پشتیبانی میکنند. این دو گزاره، فرضیه صفر و فرضیه جایگزین نامیده میشوند. نمونههای زیر نمونههای بارزی از این آزمونها هستند:
- فرضیه صفر: اثر در جمعیت وجود ندارد.
- فرضیه جایگزین: اثر در جمعیت وجود دارد.
آزمون فرضیه، عدم قطعیت ذاتی استفاده از یک نمونه برای نتیجهگیری در مورد یک جمعیت را در نظر میگیرد، که احتمال کشفهای نادرست را کاهش میدهد. این رویهها تعیین میکنند که آیا دادههای نمونه به اندازه کافی با فرضیه صفر ناسازگار هستند که بتوانید آن را رد کنید. اگر بتوانید فرض صفر را رد کنید، دادههای شما از گزاره جایگزین مبنی بر وجود یک اثر در جمعیت حمایت میکنند.
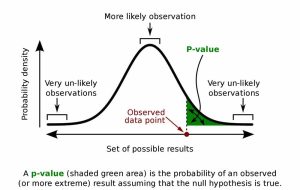
معناداری آماری در آزمون فرضیه نشان میدهد که اثری که در دادههای نمونه مشاهده میکنید، احتمالاً پس از در نظر گرفتن خطای نمونهگیری تصادفی، تغییرپذیری و اندازه نمونه، در جمعیت نیز وجود دارد. نتایج شما زمانی از نظر آماری معنادار هستند که مقدار p کمتر از سطح معناداری شما باشد یا به طور معادل، زمانی که فاصله اطمینان شما مقدار فرضیه صفر را حذف میکند.
برعکس، نتایج غیر معنادار نشان میدهند که با وجود یک اثر نمونه آشکار، نمیتوانید مطمئن باشید که در جمعیت وجود دارد. این میتواند یک تغییر تصادفی در نمونه باشد و نه یک اثر واقعی.
۵ مرحله آزمون معناداری
آزمون فرضیه شامل پنج مرحله کلیدی است که هر کدام برای اعتبارسنجی فرضیه تحقیق با استفاده از روشهای آماری حیاتی هستند:
- صورت بندی فرضیهها: فرضیههای تحقیق خود را به صورت فرضیه صفر (H0) و فرضیه جایگزین (HA) بنویسید.
- جمعآوری دادهها: دادههایی را که به طور خاص برای آزمون فرضیه هدفگذاری شدهاند، جمعآوری کنید.
- انجام آزمون: از یک آزمون آماری مناسب برای تجزیه و تحلیل دادههای خود استفاده کنید.
- تصمیمگیری: بر اساس نتایج آزمون آماری، تصمیم بگیرید که آیا فرضیه صفر را رد کنید یا آن را رد نکنید.
- گزارش نتایج: نتایج را در بخشهای نتایج و بحث مقاله خود خلاصه و ارائه دهید.
در حالی که جزئیات این مراحل میتواند بسته به زمینه تحقیق و نوع دادهها متفاوت باشد، فرآیند اساسی آزمون فرضیه در مطالعات مختلف ثابت میماند.
بیایید این مراحل را در یک مثال بررسی کنیم!
مثال آزمون فرضیه
محققان میخواهند مشخص کنند که آیا یک برنامه آموزشی جدید عملکرد دانشآموزان را در آزمونهای استاندارد بهبود میبخشد یا خیر. آنها به طور تصادفی 30 دانشآموز را به یک گروه کنترل که از برنامه درسی استاندارد پیروی میکنند و 30 دانشآموز دیگر را به یک گروه آزمایشی که در برنامه آموزشی جدید شرکت میکنند، اختصاص میدهند. پس از یک ترم، نمرات آزمون هر دو گروه را با هم مقایسه میکنند.
محققان فرضیههای خود را مینویسند. این گزارهها در مورد جمعیت صدق میکنند، بنابراین آنها از نماد mu (μ) برای پارامتر میانگین جمعیت استفاده میکنند.
- فرضیه صفر (H0): میانگین نمرات آزمون در جمعیت برای دو گروه برابر است (μ1 = μ2).
- فرضیه جایگزین (HA): میانگین نمرات آزمون در جمعیت برای دو گروه نابرابر است (μ1≠ μ2).
انتخاب آزمون فرضیه صحیح به ویژگیهایی مانند نوع داده و تعداد گروهها بستگی دارد. از آنجا که آنها از دادههای پیوسته استفاده میکنند و دو میانگین را با هم مقایسه میکنند، محققان از آزمون t دو نمونهای استفاده میکنند.
نتایج در اینجا آمده است.
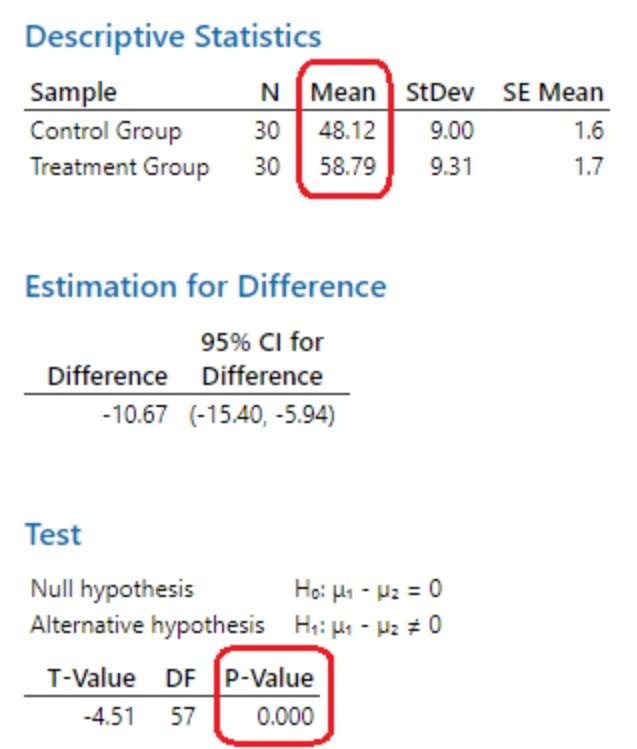
میانگین گروه آزمایش ۵۸.۷۰ است، در مقایسه با میانگین گروه کنترل ۴۸.۱۲. تفاوت میانگین ۱۰.۶۷ امتیاز است. از مقدار p و سطح معنیداری آزمون برای تعیین اینکه آیا این تفاوت احتمالاً محصول نوسانات تصادفی در نمونه است یا یک اثر واقعی جمعیت استفاده کنید.
از آنجا که مقدار p (۰.۰۰۰) کمتر از سطح معنیداری استاندارد ۰.۰۵ است، نتایج از نظر آماری معنیدار هستند و میتوانیم فرضیه صفر را رد کنیم. دادههای نمونه شواهد کافی برای نتیجهگیری مبنی بر وجود اثر برنامه جدید در جمعیت را ارائه میدهند.
محدودیتها
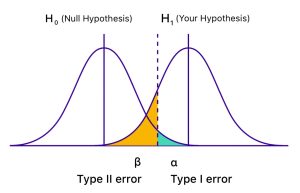
آزمون فرضیه، اثربخشی شما را در تصمیمگیریهای مبتنی بر داده بهبود میبخشد. با این حال، ۱۰۰٪ دقیق نیست زیرا نمونههای تصادفی گاهی اوقات نتایج تصادفی تولید میکنند. آزمونهای فرضیه دو نوع خطا دارند که هر دو مربوط به نتیجهگیریهای نادرست هستند.
- خطای نوع اول: آزمون یک فرضیه صفر واقعی – یک مثبت کاذب – را رد میکند.
- خطای نوع دوم: آزمون یک فرضیه صفر کاذب – یک منفی کاذب – را رد نمیکند.
درباره خطاهای نوع اول و نوع دوم بیشتر بدانید.
بررسی ما از آزمون فرضیه با استفاده از یک مثال عملی از یک برنامه آموزشی، توانایی قدرتمند آن را در هدایت تصمیمات بر اساس شواهد آماری نشان میدهد. چه دانشجو، محقق یا متخصص باشید، درک و بهکارگیری این رویهها میتواند درهای جدیدی را برای کشف بینشها و تصمیمگیریهای آگاهانه باز کند. اجازه دهید این ابزار تلاشهای تحلیلی شما را در حین پیمایش در دریاهای وسیع دادهها تقویت کند.




پاسخگوی سوالات و نظرات شما هستیم