آزمون شاپیرو-ویلک (Shapiro-Wilk test)

آزمون شاپیرو-ویلک نوعی آزمون فرض است که بر روی نمونه‌ای اعمال می‌شود که فرضیه صفر (Null) آن این است که نمونه از توزیع نرمال تبعیت می کند.

دانشمندان داده معمولاً باید بررسی کنند که آیا داده‌ها به صورت نرمال توزیع شده‌اند یا خیر. به عنوان مثال، بررسی نرمال بودن باقیمانده‌های رگرسیون خطی به منظور استفاده صحیح از آزمون F است. یکی از راه‌های انجام این کار از طریق آزمون شاپیرو-ویلک است که یک آزمون فرضیه است که بر روی نمونه‌ای با فرضیه صفر مبنی بر اینکه نمونه از توزیع نرمال ناشی می‌شود، اعمال می‌شود.

به طور خلاصه، آزمون شاپیرو-ویلک یک آزمون فرض است که ارزیابی می‌کند آیا یک مجموعه داده دارای توزیع نرمال است یا خیر. این آزمون، داده‌های یک نمونه را با فرضیه صفر مبنی بر نرمال بودن توزیع مجموعه داده‌ها ارزیابی می‌کند. مقدار p بزرگ نشان می‌دهد که مجموعه داده‌ها دارای توزیع نرمال هستند، و مقدار p پایین نشان می‌دهد که توزیع نرمال ندارند.

مثلا شکل زیر یک توزیع نرمال دارد:

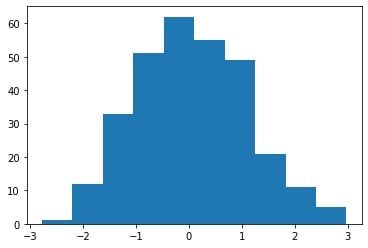
مثال زیر، توزیع غیرنرمال را نشان می دهد:

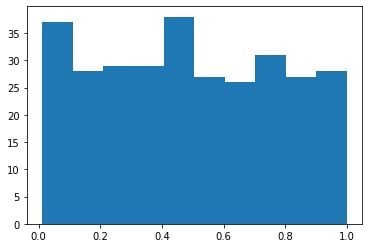
نرمال بودن چیست؟

نرمال بودن به این معنی است که یک نمونه خاص از یک توزیع گاوسی تولید شده است که لزوماً نباید یک توزیع نرمال استاندارد با میانگین صفر و واریانس برابر با یک باشد.

چندین موقعیت وجود دارد که دانشمندان داده ممکن است به داده‌های با توزیع نرمال نیاز داشته باشند:

• برای مقایسه باقیمانده‌های رگرسیون خطی در آزمون آموزش با باقیمانده‌های مجموعه آزمون با استفاده از آزمون F.
• برای مقایسه میانگین مقدار یک متغیر در گروه‌های مختلف با استفاده از آزمون تحلیل واریانس یک طرفه (ANOVA) یا آزمون t-student.
• برای ارزیابی همبستگی خطی بین دو متغیر با استفاده از یک آزمون مناسب روی ضریب همبستگی پیرسون آنها.
• برای ارزیابی اینکه آیا احتمال یک ویژگی در برابر یک هدف در یک مدل Naive Bayes به ما اجازه می‌دهد از یک مدل طبقه‌بندی Naive Bayes گاوسی استفاده کنیم یا خیر.

اینها همه مثال‌های مختلفی هستند که ممکن است به طور مکرر در کار روزمره یک دانشمند داده اتفاق بیفتند.

متأسفانه، داده‌ها همیشه به طور نرمال توزیع نمی‌شوند. اگرچه، می‌توانیم برخی تبدیل‌های خاص را برای متقارن‌تر کردن توزیع، مانند تبدیل توان، اعمال کنیم.

یک راه خوب برای ارزیابی نرمال بودن یک مجموعه داده، استفاده از نمودار Q-Q است که به ما یک تجسم گرافیکی از نرمال بودن می‌دهد. اما ما اغلب به یک نتیجه کمی برای بررسی نیاز داریم و یک نمودار نمی‌تواند کافی باشد. به همین دلیل است که می‌توانیم از یک آزمون فرض برای ارزیابی نرمال بودن یک نمونه استفاده کنیم.

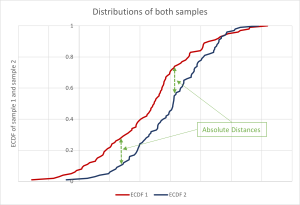
فرق بین آزمون شاپیرو-ویلک و کولموگروف-اسمیرنوف

آزمون شاپیرو-ویلک برای حجم نمونه کم (کمتر از ۵۰ نمونه) روش مناسب‌تری است، اگرچه می‌توان آن را برای حجم نمونه بیشتر نیز به کار برد، در حالی که آزمون کولموگروف-اسمیرنوف برای n ≥۵۰ استفاده می‌شود.

(خلاصه) آزمون شاپیرو-ویلک چیست؟

آزمون شاپیرو-ویلک یک آزمون فرضیه است که بر روی نمونه‌ای با فرضیه صفر مبنی بر اینکه نمونه از توزیع نرمال تولید شده است، اعمال می‌شود. اگر مقدار p پایین باشد، می‌توانیم چنین فرضیه صفری را رد کنیم و بگوییم که نمونه از توزیع نرمال تولید نشده است.

این یک ابزار آماری آسان برای استفاده است که می‌تواند به ما در یافتن پاسخی برای بررسی نرمال بودن مورد نیاز کمک کند، اما یک نقص دارد: با مجموعه داده‌های بزرگ به خوبی کار نمی‌کند. حداکثر اندازه مجاز برای یک مجموعه داده به پیاده‌سازی بستگی دارد، اما مثلا در پایتون می‌بینیم که اندازه نمونه بزرگتر از ۵۰۰۰، محاسبه تقریبی مقدار p را به ما می‌دهد.

مزایای آزمون شاپیرو-ویلک

آزمون شاپیرو-ویلک برای نرمال بودن، ابزاری آماری با کاربرد بسیار ساده برای ارزیابی نرمال بودن یک مجموعه داده است. خیلی از افراد معمولاً آن را پس از ایجاد یک مجموعه تجسم داده یا از طریق هیستوگرام و/یا نمودار Q-Q اعمال می‌کنند. این یک ابزار بسیار مفید برای اطمینان از برآورده شدن الزام نرمال بودن در هر زمانی است که به آن نیاز داریم و باید در جعبه ابزار هر دانشمند داده ای وجود داشته باشد.

مطالب مرتبط مفید

آزمون کولموگروف- اسمیرنوف

آزمون نرمال بودن داده ها (Normality Test)

روش تحقیق آزمایشی یا تجربی