مغالطه عطف منطقی
مغالطهی عطف منطقی چیست؟
مغالطهی عطف منطقی (Conjunction Fallacy) یک سوگیری شناختی است که زمانی رخ میدهد که کسی به اشتباه معتقد باشد دو رویداد که با هم رخ میدهند، احتمال بیشتری نسبت به هر یک از آن دو رویداد به تنهایی دارند. به عبارت دیگر، این باور اشتباه است که یک نتیجهی چندوجهی و کاملا باجزئیات، احتمال بیشتری برای وقوع دارد تا یک نسخهی کلیتر از آن نتیجه.
این پدیده اغلب زمانی رخ میدهد که افراد به جای ارزیابی احتمال هر رویداد به طور مستقل، بر چگونگی ارتباط دو رویداد تمرکز میکنند. این تمرکز بر تعامل بین رویدادها میتواند منجر به قضاوتهای ناقص یا گمراهکننده شود، زیرا توجه را از در نظر گرفتن احتمالات واقعی رویدادهای منفرد منحرف میکند.
مغالطهی ربط میتواند به طور قابل توجهی قضاوت و فرآیندهای تصمیمگیری ما را منحرف کند. با سوق دادن ما به سمت بیش از حد ارزش دادن به احتمال رویدادهای همزمان، ممکن است منجر به درک اغراقآمیز از احتمال آنها شود. این قضاوت نادرست میتواند ما را برای نتایج آماده نکند، زیرا انتظارات ما با واقعیت احتمالات مربوطه همسو نیست.
مثال مغالطهی عطف: مسئلهی لیندا
در اینجا مثال کلاسیک مغالطهی عطف منطقی در ادبیات، که به عنوان مسئلهی لیندا شناخته میشود، آورده شده است.
لیندا ۳۱ ساله، مجرد، بسیار باهوش و رکگو است. او در رشتهی فلسفه تحصیل کرده است. او در دوران دانشجویی، دانشجوی فلسفه بود و عمیقاً نگران تبعیض و مسائل عدالت اجتماعی بود و در تظاهرات ضد هستهای شرکت میکرد.
بر اساس توضیحات، کدام یک از دو جملهی زیر محتملتر است؟
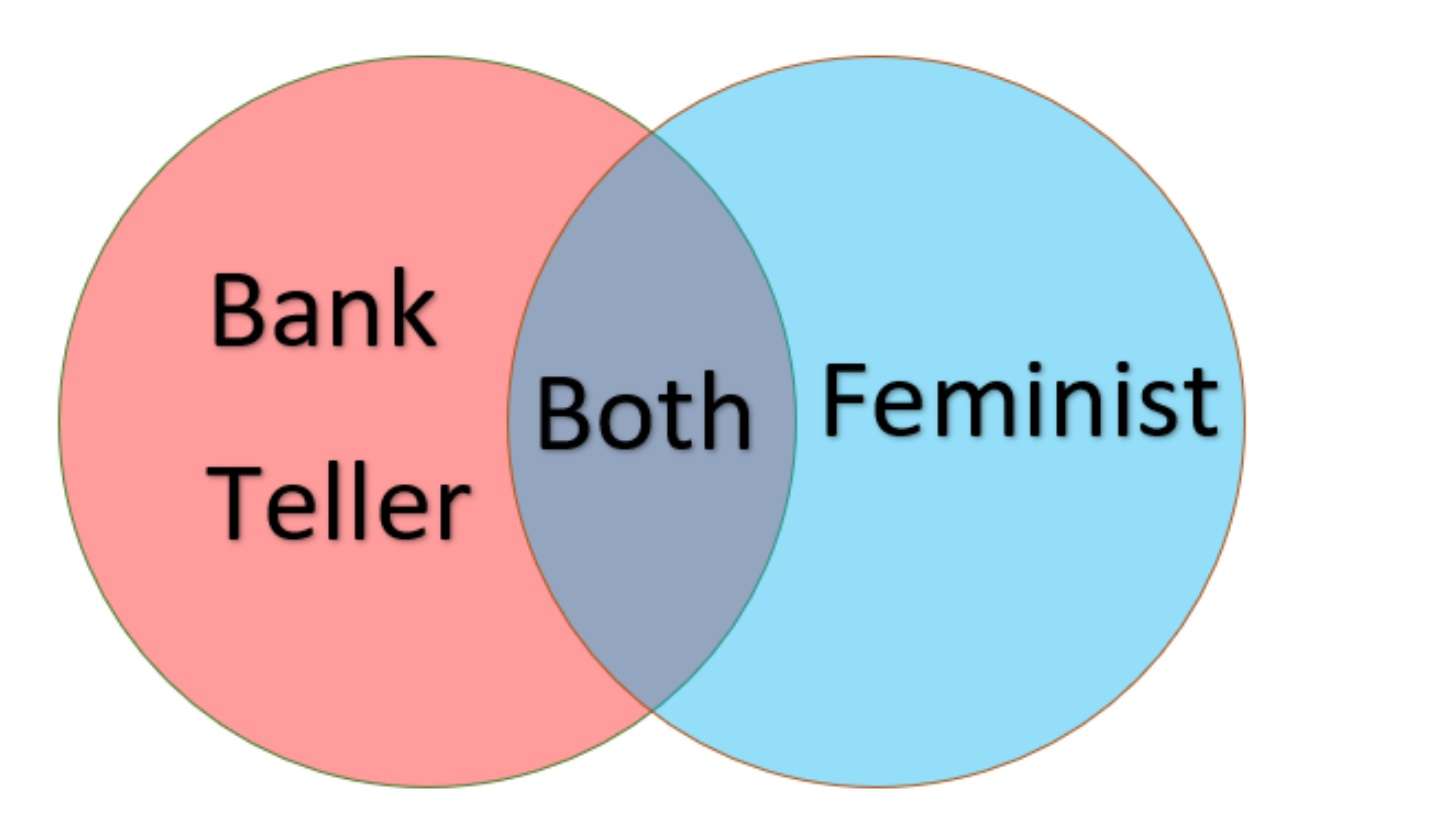
- لیندا یک صندوقدار بانک است.
- لیندا یک صندوقدار بانک است و در جنبش فمینیستی فعال است.
پاسخ صحیح شماره ۱ است. با این حال، بسیاری گزینه ۲ را انتخاب میکنند زیرا با توجه به پیشینه لیندا، محتملتر به نظر میرسد. به طور خاص، در مطالعه اولیهای که توسط تورسکی و کانمن انجام شد، حدود ۸۵٪ از شرکتکنندگان این گزینه را انتخاب کردند، با وجود اینکه از نظر آماری احتمال کمتری نسبت به گزینه ۱ (لیندا فقط یک صندوقدار بانک بودن) داشت. این نتیجه قابل توجه، جذابیت شهودی روایتهای دقیق را نسبت به استدلال آماری، که جنبه کلیدی مغالطه عطف منطقی است، برجسته میکند.
احتمال وقوع دو رویداد همزمان (لیندا یک صندوقدار بانک بودن و یک فمینیست فعال بودن) همیشه برابر یا کمتر از احتمال وقوع هر یک به تنهایی است. دلیل این امر در بخش بعدی بیشتر توضیح داده خواهد شد!
چرا باید کمتر از یا مساوی باشد؟
جهانی را تصور کنید که در آن هر کارمند بانک فمینیست باشد – این یک احتمال ۱۰۰٪ است. در این سناریو، همه کارمندان بانک نیز فمینیست هستند. از این رو، شانس لیندا برای اینکه هم کارمند بانک باشد و هم فمینیست، دقیقاً برابر با شانس او برای کارمند بانک بودن است زیرا اعداد برابر هستند.
با این حال، در هر موقعیتی که احتمال ۱۰۰٪ کامل نباشد، همه کارمندان بانک فمینیست نیستند. در این حالت، تعداد کارمندان بانک فمینیست کمتر از تعداد کل کارمندان است. از این رو، احتمال اینکه لیندا هم کارمند بانک باشد و هم فمینیست (گزینه ۲) کمتر از احتمال اینکه لیندا فقط کارمند بانک باشد، است.
بنابراین، از دیدگاه آماری، احتمال بیشتری وجود دارد که لیندا صرفاً یک کارمند بانک باشد. ریاضیات به ما میگوید که اضافه کردن جزئیات بیشتر (مانند فمینیست فعال بودن) این احتمال را کاهش میدهد، حتی زمانی که به نظر میرسد آن جزئیات کاملاً با شخصیت لیندا همسو هستند.
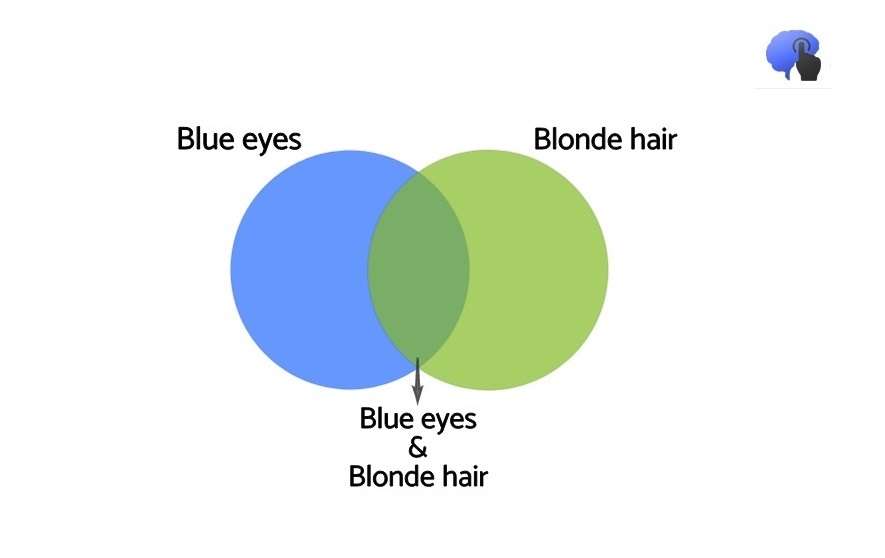
دایرهی صندوقدار بانک شامل تمام افرادی است که فقط صندوقدار هستند و کسانی که هم صندوقدار هستند و هم فمینیست. این ترکیب زیرمجموعهای است که نمیتواند بزرگتر از صندوقدارها باشد. حتی اگر دو دایره طوری همپوشانی داشته باشند که تمام صندوقدارهای بانک فمینیست باشند، آن تعداد نمیتواند بزرگتر از تعداد صندوقدارها باشد! این با سناریوی احتمال ۱۰۰٪ قبلی مطابقت دارد.
به راحتی میتوان فکر کرد که یک شرط خاصتر محتملتر از یک شرط گستردهتر است زیرا این ترکیب درست به نظر میرسد. اما اینگونه است که مغالطهی ربط ما را به اشتباه میاندازد. نمودار ون حقیقت را نشان میدهد: شرط گستردهتر فضای بیشتری برای وقوع دارد. این خلاف شهود است – هر چه جزئیات بیشتری اضافه کنید، احتمال وقوع چیزی کمتر میشود، حتی اگر باورپذیرتر به نظر برسد.
مغز ما روایت را بر احتمالات آماری ترجیح میدهد! از این نظر، مغالطهی عطف منطقی شبیه مغالطهی نرخ پایه است.
چرا این خطا رخ میدهد؟
تورسکی و کانمن معتقدند که مغالطهی ربط ناشی از اتکای ما به یک میانبر ذهنی است که به عنوان روش اکتشافیِ بازنمایی شناخته میشود. این رویکرد شامل قضاوت بر اساس میزان شباهت یک گزینه به تصویر ذهنی یا کلیشهی ماست. در مورد لیندا، گزینهی ۲ مناسبتر یا «بازنمایندهتر» از تصویر دقیقی است که از او ترسیم شده است و همین امر باعث میشود بسیاری آن را انتخاب کنند. این احساس حتی با وجود اینکه از دیدگاه صرفاً ریاضی، گزینهی ۲ احتمال کمتری دارد، اتفاق میافتد. این بینش روشن میکند که چگونه برداشتها و سوگیریهای ما میتوانند بر احتمال منطقی در تصمیمگیری غلبه کنند.
همه چیز در مورد چگونگی درک احتمالات و اجازه دادن به جزئیات خاص برای تحریف قضاوت ما است.
برای جلوگیری از مغالطهی ربط، به جای اینکه درگیر چگونگی ارتباط این رویدادها با یکدیگر شوید، احتمال هر رویداد را بر اساس شایستگیهای خود آن ارزیابی کنید. با ارزیابی روشمند احتمال هر اتفاق، میتوانید ارزیابیها و تصمیمات بهتری بگیرید، فارغ از تأثیر گمراهکنندهی ارتباطات درک شده بین رویدادها.
مثال دوم مغالطهی ربط
یک بررسی جامع سلامت شامل گروه متنوعی از مردان بالغ اهل بریتیش کلمبیا، با سنین و حرفههای مختلف بود.
آقای ف. نیز در این گروه قرار داشت که به طور تصادفی از فهرست شرکتکنندگان انتخاب شده بود.
در نظر بگیرید کدام یک از این سناریوها محتملتر است: (یکی را انتخاب کنید)
ف. حداقل یک حمله قلبی را تجربه کرده است.
ف. حداقل یک حمله قلبی را تجربه کرده است و بالای ۵۵ سال سن دارد.
شرط میبندم در این مورد بهتر عمل کردید!
از آنجا که احتمال وقوع رویدادهای ترکیبی هرگز نمیتواند از احتمال وقوع رویدادهای منفرد بیشتر باشد، منطقاً، گزینه اول از نظر آماری محتملتر است.
در این پست سایت، ما به مفهوم جذاب مغالطهی عطف منطقی پرداختیم. در این خطای شناختی رایج، افراد به اشتباه فرض میکنند که چندین شرط خاص محتملتر از یک شرط هستند. افزودن جزئیات بیشتر به یک سناریو، در حالی که آن را محتملتر جلوه میدهد، در واقع احتمال آن را کاهش میدهد. این کاوش، روشهای ظریف عملکرد ذهن ما و اهمیت تفکر انتقادی در تصمیمگیریهای روزمره را روشن میکند.




پاسخگوی سوالات و نظرات شما هستیم