بازگشت به میانگین: تعریف و مثالها

بازگشت به میانگین چیست؟

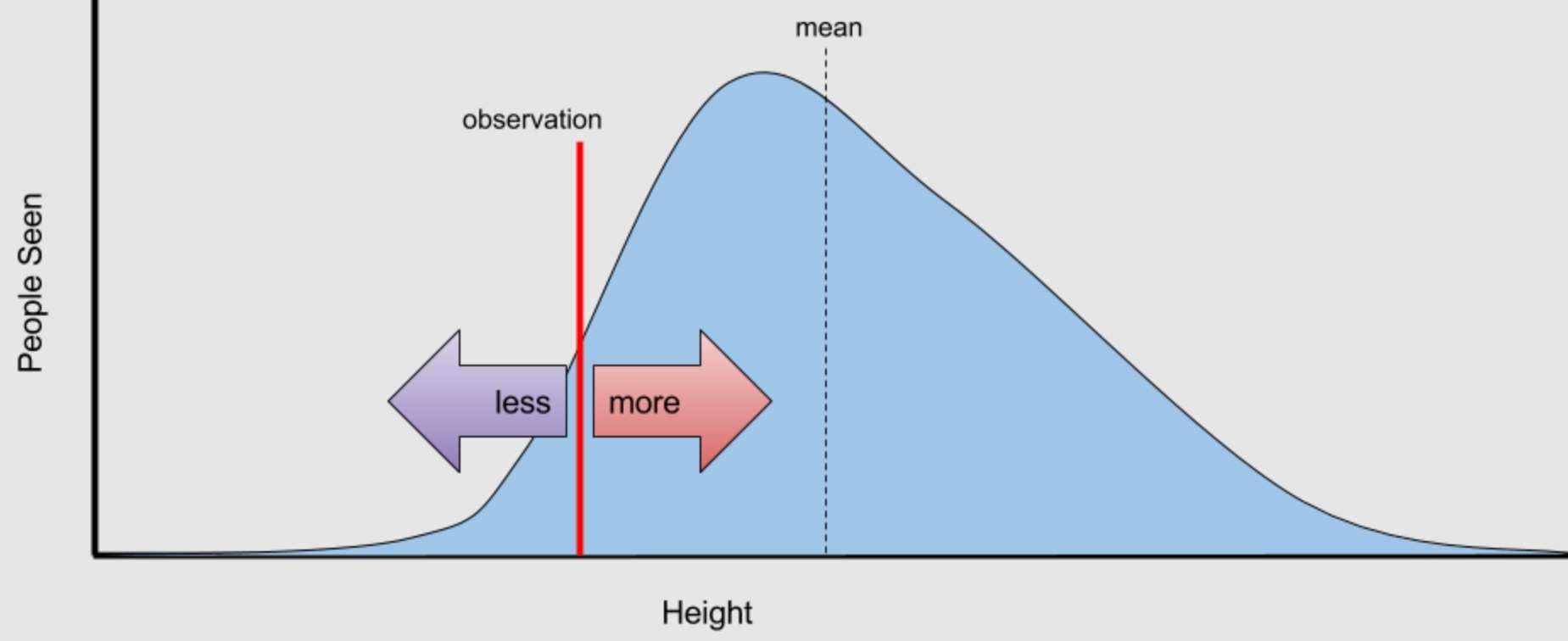
بازگشت یا رگرسیون به میانگین (Regression to the Mean)، تمایل آماری برای یک نمونه یا مقدار مشاهده شده افراطی است که پس از آن یک نمونه یا مقدار متوسط‌تر قرار می‌گیرد. و تمایل به مشاهده بعدی برای نزدیک‌تر شدن به میانگین پس از یک مقدار حدی یا افراطی را برجسته می‌کند. این مفهوم فقط برای تغییرات تصادفی در یک فرآیند یا سیستم اعمال می‌شود و به مداخلات یا رویدادهایی که بر نتیجه تأثیر می‌گذارند، مربوط نمی‌شود.

به طور خلاصه، موارد پرت و خوش‌شانس احتمالاً پس از رویدادهای معمولی‌تر رخ می‌دهند.

به عنوان مثال، فرض کنید کلاس‌هایی از دانش‌آموزان در یک آزمون استاندارد شرکت می‌کنند و میانگین نمره یک کلاس 75٪ است. اگر میانگین دانش‌آموزان یک کلاس 90٪ باشد، کلاس بعدی احتمالاً پایین‌تر و نزدیک‌تر به میانگین خواهد بود. برعکس، اگر میانگین یک کلاس 60٪ باشد، کلاس بعدی احتمالاً بالاتر خواهد بود.

در آمار، “بازگشت به میانگین” یک مفهوم مهم است که توضیح می‌دهد چرا نتایج حدی یا افراطی اغلب در اندازه‌گیری‌های بعدی با نتایج متوسط‌تر دنبال می‌شوند. این یک اتفاق طبیعی است که نیازی به مداخله ندارد. اگر چیزی را به طور غیرمعمول بالا یا پایین مشاهده کنید، احتمالاً دفعه بعد که آن را اندازه‌گیری می‌کنید، به میانگین نزدیک‌تر خواهد بود.

بازگشت به میانگین فقط یک مفهوم نظری نیست، بلکه یک مفهوم عملی با پیامدهای قابل توجه است. چه یک عملکرد شگفت‌انگیز در ورزش باشد، چه یک تغییر ناگهانی در بازار سهام، یا تغییر در نمرات آزمون‌های استاندارد، مفهوم رگرسیون به میانگین برقرار است و نتایج را به میانگین نزدیک‌تر می‌کند.

بیایید درباره این مفهوم آماری جذاب و دلیل وقوع آن بیشتر بدانیم، پیامدهای آن را بررسی کنیم و دلیل اهمیت آن در تحقیق را بررسی کنیم.

مثال‌های بازگشت به میانگین

مثال‌های زیر مفهوم آماری رگرسیون به میانگین را در زمینه‌های مختلف نشان می‌دهند. در همه این موارد، ممکن است کسی به دنبال یک علت اساسی باشد که باعث ایجاد تغییر شده است، اما می‌تواند فقط یک محصول جانبی طبیعی از تغییرات تصادفی باشد.

عملکرد ورزشی

ورزش می‌تواند منبع بسیار خوبی برای رگرسیون باشد تا با تمام آمارهایی که ثبت می‌کند، معنی پیدا کند!

یک بازیکن بسکتبال در یک بازی به طور غیرمعمولی امتیاز بالایی کسب می‌کند، اما در مسابقه بعدی به میانگین امتیاز خود برمی‌گردد.

این ایده همچنین می‌تواند در کل فصل‌ها صدق کند زیرا می‌توانید یک فصل را به عنوان نمونه‌ای از بازی‌ها در نظر بگیرید. یک تازه‌کار می‌تواند فصل اول فوق‌العاده خوبی داشته باشد و سپس “افت عملکرد سال دوم” را تجربه کند، که در آن عملکرد به سمت میانگین کاهش می‌یابد. برعکس، بازیکنان بیسبال با میانگین ضربه‌های ضعیف در یک فصل، تمایل دارند فصل بعد به سمت میانگین بهبود یابند.

سرمایه‌گذاری در سهام با عملکرد بالا

یک سرمایه‌گذار طیف وسیعی از سهام را برای سبد سهام خود انتخاب می‌کند زیرا آنها در یک فصل به طور غیرمعمول خوب عمل کرده‌اند. با این حال، در فصل بعد، عملکرد این سهام به سطوح متوسط ​​​​تری کاهش می‌یابد که نشان دهنده رفتار معمول بازار است. بازگشت به میانگین در عمل!

مراجعات به اورژانس بیمارستان

طی یک هفته، اورژانس یک بیمارستان به طور قابل توجهی بیماران کمتری نسبت به میانگین می‌بیند، ظاهراً بدون هیچ دلیل خاصی. هفته بعد، تعداد بیماران به میانگین معمول برمی‌گردد و با تغییرات تصادفی معمول در مراجعه به اورژانس همسو می‌شود.

سیاست نمره آزمون استاندارد

تلاش ماساچوست در سال ۱۹۹۹ برای بهبود نمرات آزمون استاندارد، نمونه‌ای از بازگشت به میانگین است. در آن سال، به مدارس اهدافی برای بهبود نمرات آزمون متوسط ​​​​داده شد. بسیاری از مدارس با عملکرد پایین به اهداف خود دست یافتند. این سیاست در ابتدا موفقیت‌آمیز به نظر می‌رسید. با این حال، بسیاری از مدارس برتر در رسیدن به اهداف خود شکست خوردند. به نظر می‌رسد این وضعیت، بازگشت به میانگین است، جایی که نمرات شدید به طور طبیعی به میانگین نزدیک‌تر می‌شوند.

تحسین در مقابل انتقاد

در محیط‌های آموزشی، مربیان اغلب از افراد ضعیف انتقاد می‌کنند و از افراد با عملکرد بالا تمجید می‌کنند. علاوه بر این، ناظران متوجه شده‌اند که بدترین افراد عملکرد بهتری دارند در حالی که افراد برتر عملکرد بدتری دارند. این الگو منجر به این نتیجه‌گیری اشتباه می‌شود که انتقاد بیشتر از تحسین، عملکرد را افزایش می‌دهد.

تا اینجا، می‌توانید ببینید که این الگو احتمالاً به دلیل بازگشت به میانگین بوده است!

مغالطه بازگشت به میانگین در تحقیق

مغالطه بازگشت به میانگین در تحقیق زمانی رخ می‌دهد که تحلیلگران به اشتباه تغییرات در نتیجه را به دستکاری‌های یک عامل آزمایشی نسبت می‌دهند، نه مشاهداتی که به میانگین بازمی‌گردند. این مغالطه نادیده می‌گیرد که چگونه نتایج غیرمعمول به دلیل شانس تصادفی به سمت میانگین تغییر می‌کنند و باعث بهبود ظاهری می‌شوند.

برای روشن شدن موضوع، مطالعه‌ای را در نظر بگیرید که در آن محققان فشار خون را اندازه‌گیری کرده و افرادی را با مقادیر غیرمعمول بالا انتخاب می‌کنند. مقادیر اولیه بالاتر از حد متوسط ​​می‌تواند تا حدی به دلیل شانس تصادفی باشد که باعث می‌شود وضعیت اساسی بدتر به نظر برسد. در نتیجه، وقتی بعداً این افراد را دوباره آزمایش می‌کنند، احتمالاً مقادیر فشار خون آنها به سمت سطوح معمول‌تر تغییر می‌کند و ظاهری از بهبود ایجاد می‌کند.

اگر محققان عجولانه نتیجه بگیرند که این تغییر کاملاً به دلیل مداخله آنها بوده است، در دام مغالطه بازگشت به میانگین می‌افتند. کاهش بعدی می‌تواند تا حدی به دلیل نوسانات طبیعی و تصادفی در فشار خون باشد. این شانس تصادفی جدا از هرگونه تغییر عمدی در متغیرهای مطالعه است.

در آزمایش‌هایی که افراد با ویژگی‌های افراطی را هدف قرار می‌دهند، از جمله یک گروه کنترل با صفات حدی یا افراطی مشابه، در نظر گرفتن رگرسیون به میانگین بسیار مهم است. این رویکرد به تمایز بین اثرات ناشی از مداخله و اثرات ناشی از رگرسیون به میانگین کمک می‌کند. علاوه بر این، اندازه‌گیری‌های مکرر در طول زمان می‌تواند به تعیین اینکه آیا مقادیر افراطی اولیه نوسانات تصادفی بوده‌اند یا بخشی از یک روند ثابت کمک کند. این کار بهتر از تکیه بر یک اندازه‌گیری افراطی واحد است!

درک و توجیه مغالطه بازگشت به میانگین، جنبه‌ای حیاتی از تحقیق است. این مغالطه در مورد اجتناب از دام نتیجه‌گیری نادرست از داده‌هایی است که به سادگی به میانگین خود برمی‌گردند.

چرا رگرسیون به میانگین رخ می‌دهد؟

شما نمونه‌های بازگشت به میانگین را دیده‌اید و می‌دانید که به دلیل تغییرات تصادفی رخ می‌دهد، اما دقیقاً چگونه؟ بیایید نگاهی بیندازیم!

اول و مهمتر از همه، این گرایش مبتنی بر احتمالات مربوط به توزیع‌های نمونه‌گیری است. این امر نشان‌دهنده حافظه یا تنظیم عمدی در سیستم نیست. افراد ممکن است گیج شوند زیرا به نظر می‌رسد که با فراخوانی یک مکانیسم متعادل‌کننده که رویدادهای گذشته را به خاطر می‌آورد، با مغالطه قمارباز مقابله می‌کند. اما اینطور نیست!

رگرسیون به میانگین حاصل توزیع ثابتی از مقادیر است که در آن احتمال وقوع مقادیر حدی کمتر از مقادیر مرکزی است. در نتیجه، توزیع‌های احتمال می‌توانند این پدیده را مدل‌سازی کنند. ما این کار را در بخش بعدی انجام خواهیم داد!

مثال عملی رگرسیون به میانگین

بیایید ببینیم که رگرسیون به میانگین چگونه با یک مثال عملی رخ می‌دهد. برای این مثال، من از توزیع نمرات IQ استفاده می‌کنم که از توزیع نرمال با میانگین ۱۰۰ و انحراف معیار ۱۵ پیروی می‌کند.

تصور کنید که محققان ۵ شرکت‌کننده را به طور تصادفی از این توزیع انتخاب می‌کنند و میانگین IQ 90 را محاسبه می‌کنند. می‌توانیم از توزیع نمونه‌گیری میانگین‌ها برای محاسبه احتمال اینکه نمونه بعدی ۵ نفره میانگینی نزدیک‌تر به میانگین جمعیت ۱۰۰ داشته باشد، استفاده کنیم.

نتایج

در زیر توزیع نمونه‌گیری برای نمرات IQ برای حجم نمونه پنج نفره آمده است. از آنجا که این یک توزیع نمونه‌گیری است، هر نقطه روی منحنی مربوط به میانگین‌های نمونه است، نه مقادیر فردی. ما یک تحلیل دو طرفه انجام می‌دهیم زیرا میانگین نمونه ۱۱۰ به همان اندازه میانگین نمونه ۹۰، فقط در جهت مخالف میانگین، حدی یا افراطی است.

ناحیه سایه‌دار در نمودار، میانگین‌های نمونه کمتر افراطی را نسبت به میانگین نمونه ۹۰ ما نشان می‌دهد. از نظر بصری، می‌توانید ببینید که چگونه بخش عمده میانگین‌های نمونه کمتر افراطی خواهند بود زیرا ناحیه سایه‌دار بسیار بزرگتر از دو ناحیه افراطی است. خلاصه اینکه، این نحوه‌ی کار رگرسیون به میانگین است.

اما نکنه خیلی جالب این است که چگونه این توزیع‌های احتمال می‌توانند آن را کمّی کنند! این نمودار نشان می‌دهد که احتمال اینکه نمونه‌ی دوم کمتر افراطی باشد، ۰.۸۶۳۹ است.

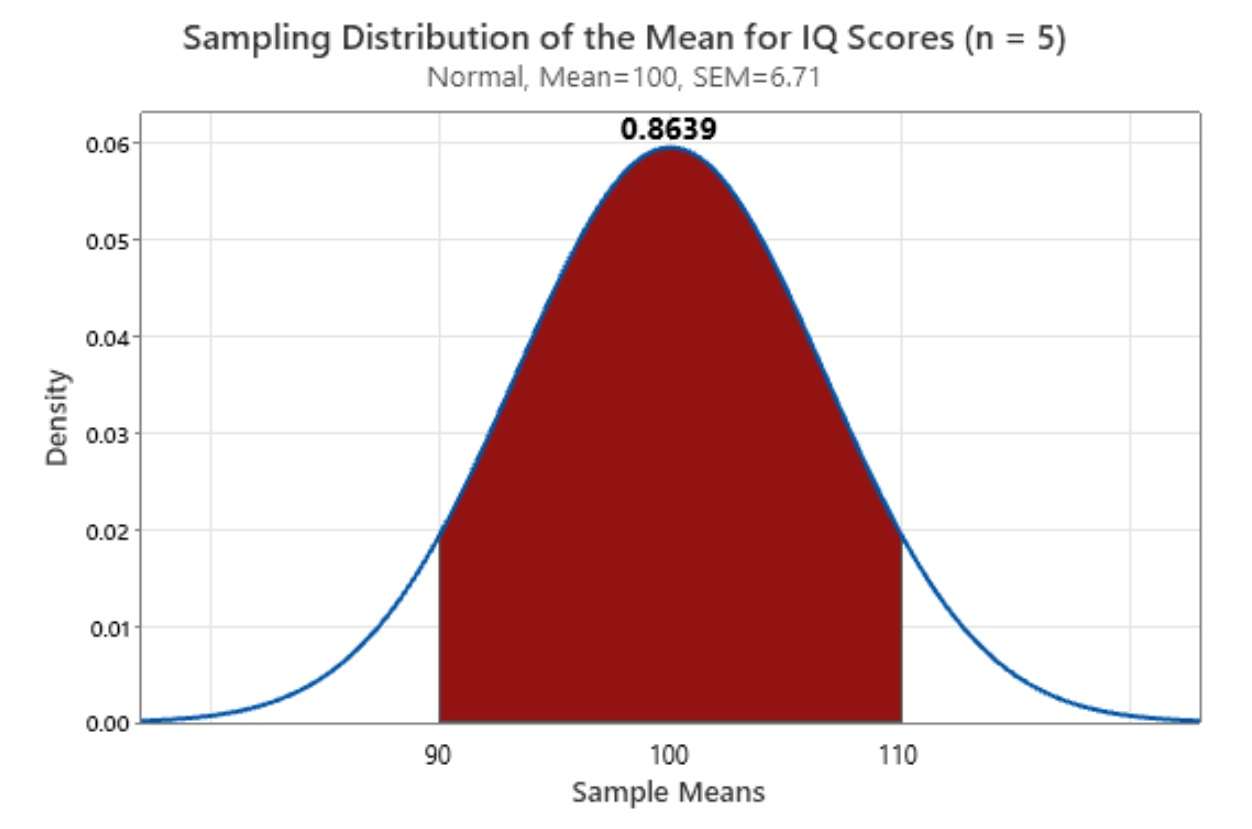
مقایسه احتمال اینکه نمونه دوم شدت کمتری داشته باشد (0.8639) با احتمال اینکه حداقل به همان اندازه شدید باشد (1 – 0.8639 = 0.1361) نشان می‌دهد که 6.3 برابر بیشتر احتمال دارد که شدت کمتری داشته باشد، همانطور که در زیر نشان داده شده است.

0.8639/0.1361= 6.3

میانگین نمونه ۹۰ ممکن است در مقایسه با میانگین جمعیت ۱۰۰ چندان افراطی به نظر نرسد، اما می‌توانید رگرسیون به میانگین را در عمل مشاهده کنید.

حال، فرض کنید میانگین نمونه اول ۸۵ باشد، کمی افراطی‌تر. با استفاده از همان فرآیند محاسبه، میانگین نمونه بعدی ۳۸.۴ برابر بیشتر احتمال دارد که کمتر افراطی باشد!

بازگشت به میانگین مفهومی واقعی است، حتی اگر به شانس تصادفی متکی باشد. این نتیجه طبیعی توزیع‌هایی است که در آنها مقادیر افراطی احتمال کمتری نسبت به مقادیر مرکزی دارند. مثال عملی نشان می‌دهد که این تمایل می‌تواند قابل توجه باشد. بازگشت به میانگین به اندازه کافی قدرتمند است که باید هنگام طراحی آزمایش‌ها و استفاده از داده‌هایی با مقادیر افراطی، آن را در نظر بگیرید!

مطالب مرتبط مفید

تحلیل رگرسیون

مغالطه با تکرار

مغالطه قیاس مع الفارق یا مقایسه ناقص