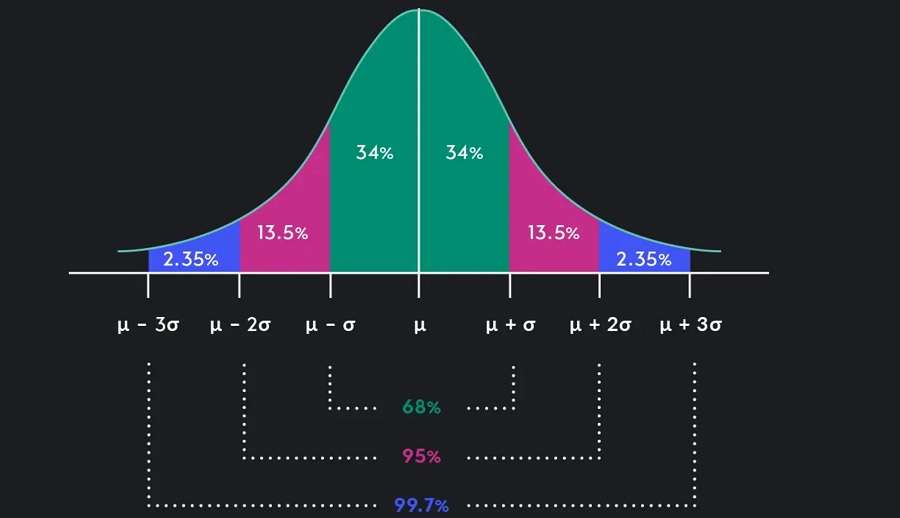
نمره استاندارد یا نمره z چیست؟

نمره z یک معیار آماری است که موقعیت یک نمره خام را بر اساس فاصله آن از میانگین، که بر حسب واحدهای انحراف معیار اندازه‌گیری می‌شود، توصیف می‌کند. نمره z مثبت نشان می‌دهد که مقدار بالاتر از میانگین قرار دارد، در حالی که نمره z منفی نشان می‌دهد که مقدار پایین‌تر از میانگین قرار دارد.

همچنین به عنوان نمره استاندارد شناخته می‌شود زیرا با استانداردسازی توزیع، امکان مقایسه نمرات متغیرهای مختلف را فراهم می‌کند. توزیع نرمال استاندارد (SND) یک توزیع نرمال با میانگین 0 و انحراف معیار (SD) 1 است (شکل 1 را ببینید).

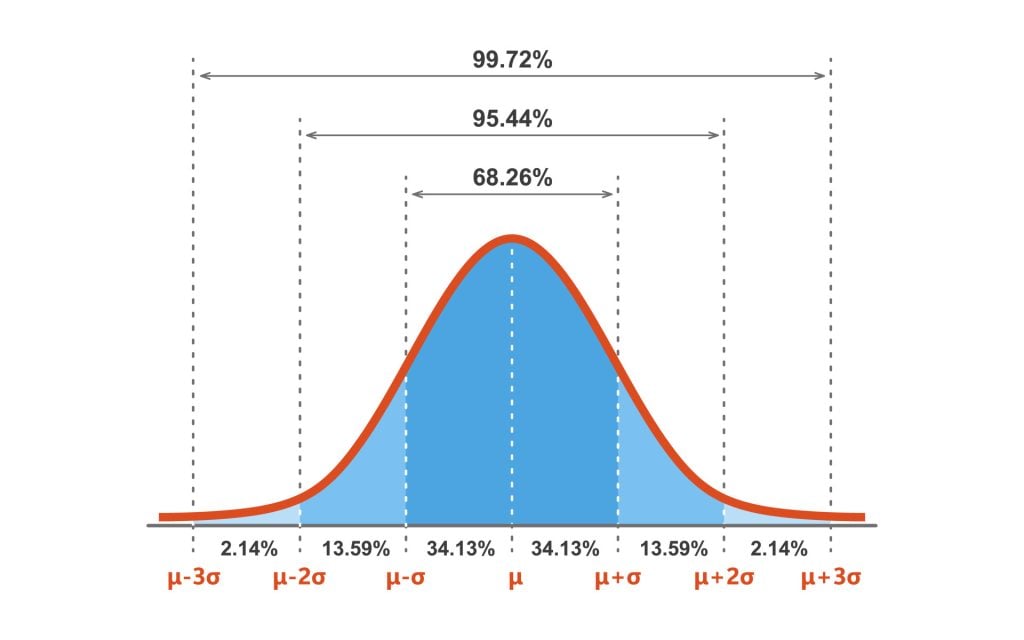
شکل ۱. توزیع نرمال استاندارد (SND).

چرا نمرات Z مهم هستند؟

استانداردسازی مقادیر (نمرات خام) یک توزیع نرمال با تبدیل آنها به نمرات z مفید است زیرا:

1. تخمین احتمال: نمرات Z می‌توانند برای تخمین احتمال وقوع یک نقطه داده خاص در یک توزیع نرمال استفاده شوند. با تبدیل نمرات z به صدک‌ها یا استفاده از یک جدول توزیع نرمال استاندارد، می‌توانید احتمال بالاتر یا پایین‌تر بودن یک مقدار از یک آستانه خاص را تعیین کنید.
2. آزمون فرضیه: نمرات Z در آزمون فرضیه برای تعیین معناداری نتایج استفاده می‌شوند. با مقایسه نمره z یک آماره نمونه با مقادیر بحرانی، می‌توانید تصمیم بگیرید که آیا یک فرضیه صفر را رد کنید یا رد نکنید.
3. مقایسه مجموعه داده‌ها: نمرات Z به شما امکان می‌دهند با استانداردسازی مقادیر، نقاط داده را از مجموعه داده‌های مختلف مقایسه کنید. این زمانی مفید است که مجموعه داده‌ها مقیاس‌ها یا واحدهای مختلفی داشته باشند.
4. شناسایی داده‌های پرت: نمرات Z به شناسایی داده‌های پرت کمک می‌کنند، که نقاط داده‌ای هستند که به طور قابل توجهی با بقیه مجموعه داده‌ها متفاوتند. معمولاً، نقاط داده‌ای با نمرات z بزرگتر از ۳ یا کمتر از -۳ به عنوان داده‌های پرت بالقوه در نظر گرفته می‌شوند و ممکن است نیاز به بررسی بیشتر داشته باشند.

نحوه محاسبه نمره استاندارد (نمره z)

فرمول محاسبه امتیاز z به صورت z = (x-μ)/σ است که در آن x امتیاز خام، μ میانگین جمعیت و σ انحراف معیار جمعیت است.

همانطور که فرمول نشان می‌دهد، امتیاز z به سادگی حاصل تقسیم امتیاز خام منهای میانگین جمعیت بر انحراف معیار جمعیت است.

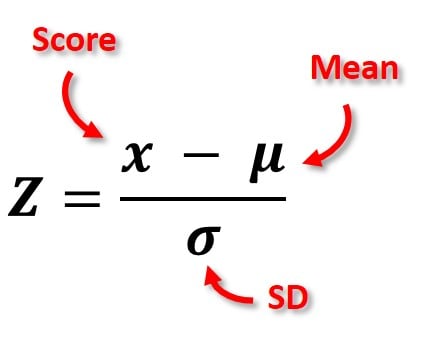
شکل ۲. فرمول نمره Z در یک جمعیت.

وقتی میانگین جمعیت و انحراف معیار جمعیت نامعلوم باشد، نمره استاندارد را می‌توان با استفاده از میانگین نمونه (x̄) و انحراف معیار نمونه (s) به عنوان تخمین‌هایی از مقادیر جمعیت محاسبه کرد.

برای محاسبه نمره z، این مراحل را دنبال کنید:

1. نمره فردی (x) را که می‌خواهید به نمره z تبدیل کنید، مشخص کنید.
2. میانگین (μ یا mu) مجموعه داده‌ها را تعیین کنید. میانگین، میانگین تمام نمرات است.
3. انحراف معیار (σ یا سیگما) مجموعه داده‌ها را محاسبه کنید. انحراف معیار، میزان پراکندگی نمرات از میانگین را اندازه‌گیری می‌کند.
4. میانگین (μ) را از نمره فردی (x) کم کنید. این به شما تفاوت بین نمره و میانگین را می‌دهد.
5. تفاوتی را که در مرحله ۴ محاسبه کردید بر انحراف معیار (σ) تقسیم کنید. نتیجه، نمره z است.

تفسیر نمره استاندارد (نمره Z)

مقدار امتیاز z به شما می‌گوید که چند انحراف معیار از میانگین فاصله دارید. مقدار مطلق بزرگتر نشان دهنده فاصله بیشتر از میانگین است.

• امتیاز z مثبت: اگر امتیاز z مثبت باشد، نشان می‌دهد که نقطه داده بالاتر از میانگین است. به عنوان مثال، امتیاز z برابر با 1.5 به این معنی است که نقطه داده 1.5 انحراف معیار بالاتر از میانگین است.
• امتیاز z منفی: اگر امتیاز z منفی باشد، نشان می‌دهد که نقطه داده زیر میانگین است. به عنوان مثال، امتیاز z برابر با -2 به این معنی است که نقطه داده 2 انحراف معیار پایین تر از میانگین است.
• امتیاز z صفر: امتیاز z برابر با صفر نشان می‌دهد که نقطه داده برابر با میانگین است.

روش دیگر برای تفسیر امتیازات z، ایجاد یک توزیع نرمال استاندارد است که به عنوان توزیع امتیاز z یا توزیع احتمال نیز شناخته می‌شود (شکل 3 را ببینید).

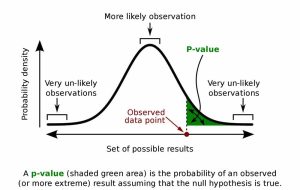
تخمین احتمال

هنگام کار با نمرات z، فرض می‌شود که داده‌ها از توزیع نرمال استاندارد با میانگین ۰ و انحراف معیار ۱ پیروی می‌کنند. این امر امکان استفاده از جداول توزیع نرمال استاندارد یا ماشین‌حساب‌ها را برای تعیین احتمالات فراهم می‌کند.

نمره z به ما می‌گوید که یک نقطه داده چند انحراف معیار از میانگین دارد. هنگامی که نمره z را بدانیم، می‌توانیم احتمال قرار گرفتن یک نقطه داده در یک محدوده خاص یا بالاتر یا پایین‌تر بودن از یک مقدار خاص را تخمین بزنیم.

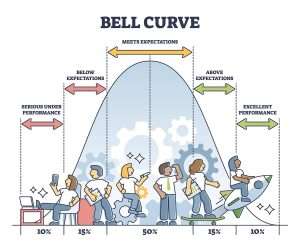
در توزیع نرمال استاندارد، یک قانون مفید به نام قانون تجربی یا قانون ۶۸-۹۵-۹۹.۷ وجود دارد. این قانون بیان می‌کند که:

• تقریباً ۶۸٪ از داده‌ها در یک انحراف معیار از میانگین قرار می‌گیرند (نمرات z بین -۱ و ۱).
• حدود ۹۵٪ از داده‌ها در دو انحراف معیار از میانگین قرار می‌گیرند (نمرات z بین -۲ و ۲).
• تقریباً ۹۹.۷٪ از داده‌ها در محدوده سه انحراف معیار از میانگین قرار می‌گیرند (نمرات z بین -۳ و ۳).

شکل ۳ نسبت توزیع نرمال استاندارد را بر حسب درصد نشان می‌دهد. همانطور که می‌بینید، احتمال ۹۵٪ برای انتخاب تصادفی نمره‌ای بین انحراف معیار -۱.۹۶ و +۱.۹۶ از میانگین وجود دارد.

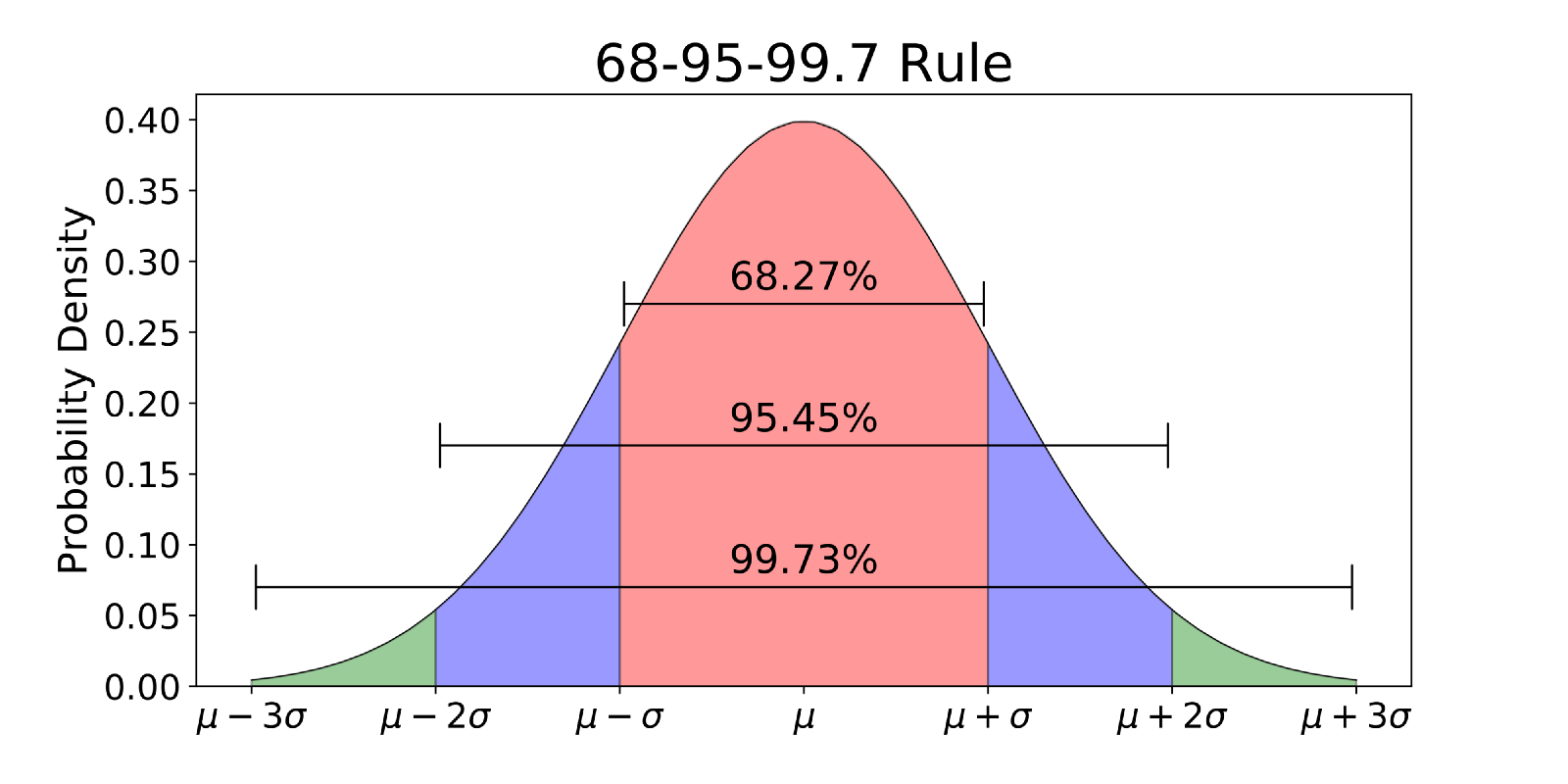
شکل ۳. نسبت توزیع نرمال استاندارد (SND) بر حسب درصد.

با استفاده از توزیع نرمال استاندارد، محققان می‌توانند احتمال به دست آوردن تصادفی یک نمره از نمونه را محاسبه کنند. به عنوان مثال، ۶۸٪ احتمال انتخاب تصادفی یک نمره بین انحراف معیار ۱- و ۱+ از میانگین وجود دارد.

آزمون فرضیه

استفاده از جدول نمره z به شما این امکان را می‌دهد که به سرعت احتمال مرتبط با یک مقدار خاص در یک مجموعه داده را تعیین کنید و به شما در تصمیم‌گیری و نتیجه‌گیری بر اساس داده‌هایتان کمک می‌کند.

اگر آزمون یک‌طرفه دارید، به دنبال ناحیه سمت چپ (برای آزمون چپ‌طرفه) یا راست (برای آزمون راست‌طرفه) نمره z خود خواهید بود.

اگر آزمون دوطرفه دارید، به دنبال ناحیه در هر دو دامنه ترکیبی خواهید بود.

سطح معنی‌داری (α) آستانه احتمال برای رد فرضیه صفر است. سطوح معنی‌داری رایج ۰.۰۱، ۰.۰۵ و ۰.۱۰ هستند. مقادیر بحرانی، نمرات z هستند که با سطح اهمیت انتخاب شده مطابقت دارند. این مقادیر را می‌توان با استفاده از یک جدول توزیع نرمال استاندارد یا ماشین حساب پیدا کرد.

جدول نمرات Z، درصد مقادیر (معمولاً یک رقم اعشاری) را در سمت چپ یک نمره Z مشخص در یک توزیع نرمال استاندارد نشان می‌دهد.

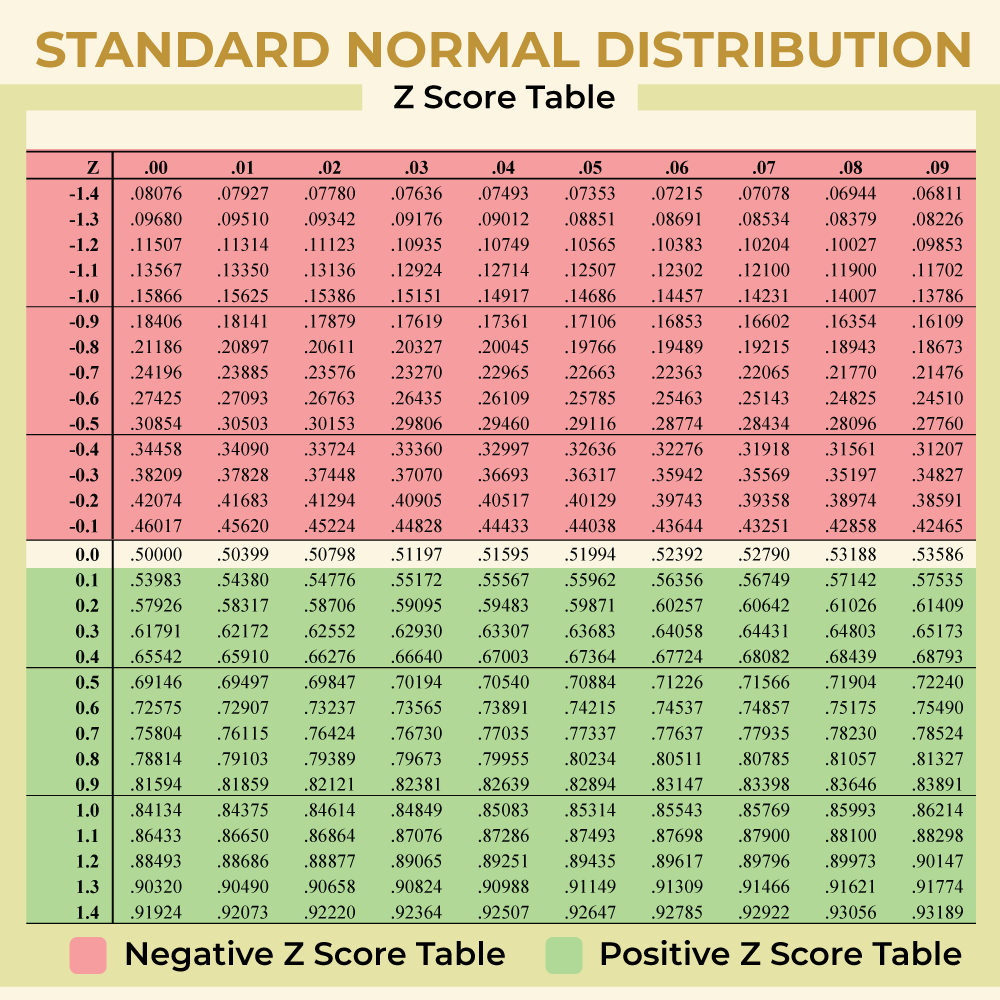
۱. بخش‌های نمره z را مشخص کنید:

نمره z از یک عدد صحیح و بخش‌های اعشاری تشکیل شده است. به عنوان مثال، اگر نمره z شما ۱.۲۴ باشد، بخش صحیح ۱ و بخش اعشاری ۰.۲۴ است.

۲. احتمال مربوطه را در جدول نمره z پیدا کنید:

• جداول نمره z معمولاً به این صورت سازماندهی می‌شوند که بخش عدد صحیح نمره z در سمت چپ‌ترین ستون و بخش اعشاری آن در ردیف بالا قرار می‌گیرد.
• بخش عدد صحیح نمره z خود را در سمت چپ‌ترین ستون پیدا کنید.
• در طول ردیف حرکت کنید تا ستونی را پیدا کنید که با بخش اعشاری نمره z شما مطابقت دارد.
• مقدار در تقاطع ردیف و ستون، احتمال (مساحت زیر منحنی) مرتبط با نمره z شما است.

۳. احتمال را تفسیر کنید:

• برای یک آزمون چپ‌دست، احتمالی که در جدول پیدا کرده‌اید، مقدار p شما است.
• برای یک آزمون راست‌دست، احتمالی را که پیدا کرده‌اید از ۱ کم کنید تا مقدار p خود را بدست آورید.
• برای یک آزمون دو‌دست، اگر اگر نمره z شما مثبت باشد، احتمال به دست آمدن مقدار p را دو برابر کنید؛ اگر نمره z شما منفی باشد، احتمال را از ۱ کم کنید و سپس نتیجه را دو برابر کنید تا مقدار p به دست آید.
• احتمال را با سطح آلفای انتخابی خود (۰.۰۵ یا ۰.۰۱) مقایسه کنید. اگر احتمال کمتر از سطح آلفا باشد، نتیجه از نظر آماری معنادار در نظر گرفته می‌شود.

در تحلیل آماری، اگر کمتر از ۵٪ احتمال انتخاب تصادفی یک نمره خام خاص وجود داشته باشد، آن نتیجه از نظر آماری معنادار در نظر گرفته می‌شود. این بدان معناست که بعید است نتیجه صرفاً به صورت تصادفی رخ داده باشد و به احتمال زیاد یک اثر یا تفاوت واقعی است.

مسائل تمرینی برای نمرات Z

نمرات z را برای موارد زیر محاسبه کنید:

نمونه سوالات نمره استاندارد (Z-SCORE)

نمرات در مقیاس بهزیستی روانشناختی از ۱ تا ۱۰ متغیر است، با میانگین نمره ۶ و انحراف معیار ۲. نمره z برای فردی که ۴ امتیاز گرفته است چقدر است؟

در سنجش اضطراب، گروهی از شرکت‌کنندگان میانگین نمره ۳۵ با انحراف معیار ۵ را نشان می‌دهند. نمره z مربوط به نمره ۳۰ چقدر است؟

یک پرسشنامه افسردگی میانگین نمره ۵۰ با انحراف معیار ۱۰ دارد. نمره z مربوط به نمره ۷۰ چقدر است؟

در یک مطالعه در مورد خواب، شرکت‌کنندگان به طور متوسط ۷ ساعت خواب در شب با انحراف معیار ۱ ساعت گزارش می‌دهند. نمره z برای فردی که ۵ ساعت خواب گزارش می‌دهد چقدر است؟ در یک آزمون حافظه، میانگین نمره ۱۰۰ با انحراف معیار ۱۵ است. نمره z مربوط به نمره ۸۵ چقدر است؟

یک مقیاس شادی میانگین نمره ۷۵ با انحراف معیار ۱۰ دارد. نمره z مربوط به نمره ۹۵ چقدر است؟

یک آزمون هوش میانگین نمره ۱۰۰ با انحراف معیار ۱۵ دارد. نمره z مربوط به نمره ۱۳۰ چقدر است؟

پاسخ‌های نمونه سوالات

پاسخ‌های خود را با این راه‌حل‌ها دوباره بررسی کنید. به یاد داشته باشید، برای هر مسئله، میانگین را از مقدار خود کم می‌کنید، سپس بر میزان تغییرات معمول مقادیر (انحراف معیار) تقسیم می‌کنید.

Z = (4 – 6) / 2 = -1

Z = (30 – 35) / 5 = -1

Z = (70 – 50) / 10 = 2

Z = (5 – 7) / 1 = -2

Z = (85 – 100) / 15 = -1

Z = (95 – 75) / 10 = 2

Z = (130 – 100) / 15 = 2

محاسبه نمره خام

گاهی اوقات، ما یک نمره z را می‌دانیم و می‌خواهیم نمره خام مربوطه را پیدا کنیم. فرمول محاسبه نمره z در یک نمونه به نمره خام در زیر آمده است:

X = (z)(SD) + میانگین

همانطور که فرمول نشان می‌دهد، نمره z و انحراف معیار در هم ضرب می‌شوند و این رقم به میانگین اضافه می‌شود.

بررسی کنید که آیا پاسخ شما منطقی است: اگر نمره z منفی داشته باشیم، نمره خام مربوطه باید کمتر از میانگین باشد و نمره z مثبت باید با نمره خام بالاتر از میانگین مطابقت داشته باشد.

محاسبه امتیاز Z با استفاده از اکسل

برای محاسبه امتیاز z یک مقدار خاص، x، ابتدا باید میانگین نمونه را با استفاده از فرمول AVERAGE محاسبه کنید.

به عنوان مثال، اگر دامنه نمرات در نمونه شما از سلول A1 شروع و به سلول A20 ختم شود، فرمول =AVERAGE(A1:A20) میانگین آن اعداد را برمی‌گرداند.

در مرحله بعد، باید انحراف معیار نمونه را با استفاده از فرمول STDEV.S محاسبه کنید.

به عنوان مثال، اگر دامنه نمرات در نمونه شما از سلول A1 شروع و به سلول A20 ختم شود، فرمول =STDEV.S (A1:A20) انحراف معیار آن اعداد را برمی‌گرداند.

حال برای محاسبه امتیاز z، فرمول زیر را در یک سلول خالی تایپ کنید: = (x – میانگین) / [انحراف معیار].

برای آسان‌تر شدن کار، به جای نوشتن مقادیر میانگین و انحراف معیار در فرمول، می‌توانید از مقادیر سلول مربوط به این مقادیر استفاده کنید. به عنوان مثال، = (A12 – B1) / [C1].

سپس، برای محاسبه احتمال یک z-score کوچکتر، که احتمال مشاهده مقداری کمتر از x (مساحت زیر منحنی سمت چپ x) است، عبارت زیر را در یک سلول خالی تایپ کنید: = NORMSDIST( و z-score محاسبه شده را وارد کنید).

برای یافتن احتمال z-score بزرگتر، که احتمال مشاهده مقداری بزرگتر از x (مساحت زیر منحنی سمت راست x) است، عبارت زیر را تایپ کنید: =1 – NORMSDIST (و z-score محاسبه شده را وارد کنید).

سوالات پرتکرار

آیا می‌توان از نمرات z با هر نوع داده‌ای، صرف نظر از توزیع آن، استفاده کرد؟

نمرات Z معمولاً برای استانداردسازی و مقایسه داده‌ها در توزیع‌های مختلف استفاده می‌شوند. آن‌ها برای داده‌هایی که از توزیع تقریباً متقارن و زنگوله‌ای شکل پیروی می‌کنند، مناسب‌ترین هستند.

با این حال، آن‌ها همچنان می‌توانند بینش‌های مفیدی برای انواع دیگر داده‌ها ارائه دهند، تا زمانی که فرضیات خاصی رعایت شوند. با این حال، برای توزیع‌های بسیار چولگی یا غیر نرمال، روش‌های جایگزین ممکن است مناسب‌تر باشند.

در نظر گرفتن ویژگی‌های داده‌ها و اهداف تحلیل هنگام تعیین اینکه آیا نمرات z مناسب هستند یا باید رویکردهای دیگری در نظر گرفته شود، مهم است.

چگونه درک نمرات z می‌تواند به تحقیقات و تحلیل آماری بهتر در روانشناسی کمک کند؟

درک نمرات z، تحقیقات و تحلیل آماری را در روانشناسی بهبود می‌بخشد. نمرات Z داده‌ها را برای مقایسه‌های معنادار استاندارد می‌کنند، داده‌های پرت را شناسایی می‌کنند و احتمال را ارزیابی می‌کنند.

آن‌ها به تفسیر اهمیت عملی، اعمال آزمون‌های آماری و نتیجه‌گیری دقیق کمک می‌کنند. نمرات Z یک معیار مشترک ارائه می‌دهند که ارتباط یافته‌ها را تسهیل می‌کند.

با استفاده از نمرات z، محققان دقت، عینیت و وضوح کار خود را بهبود می‌بخشند و منجر به درک و دانش بهتر در روانشناسی می‌شوند.

آیا می‌توان از نمره z برای تعیین احتمال وقوع یک رویداد استفاده کرد؟

خیر، نمره z به خودی خود نمی‌تواند مستقیماً احتمال وقوع یک رویداد را تعیین کند. با این حال، اطلاعاتی در مورد موقعیت نسبی یک نقطه داده در یک توزیع ارائه می‌دهد.

با تبدیل داده‌ها به نمرات z، محققان می‌توانند ارزیابی کنند که یک مقدار در مقایسه با بقیه توزیع چقدر غیرمعمول یا افراطی است. این می‌تواند به تخمین احتمال یا احتمال به دست آوردن یک نمره خاص یا مقادیر افراطی‌تر کمک کند.

بنابراین، در حالی که نمرات z بینشی در مورد نادر بودن نسبی یک رویداد ارائه می‌دهند، اما به طور مستقیم احتمال وقوع رویداد را به تنهایی تعیین نمی‌کنند.

مطالب مرتبط مفید

مقدار احتمال (p-value) و سطح معناداری

توزیع نرمال (منحنی زنگوله ای)

آزمون نرمال بودن داده ها (Normality Test)