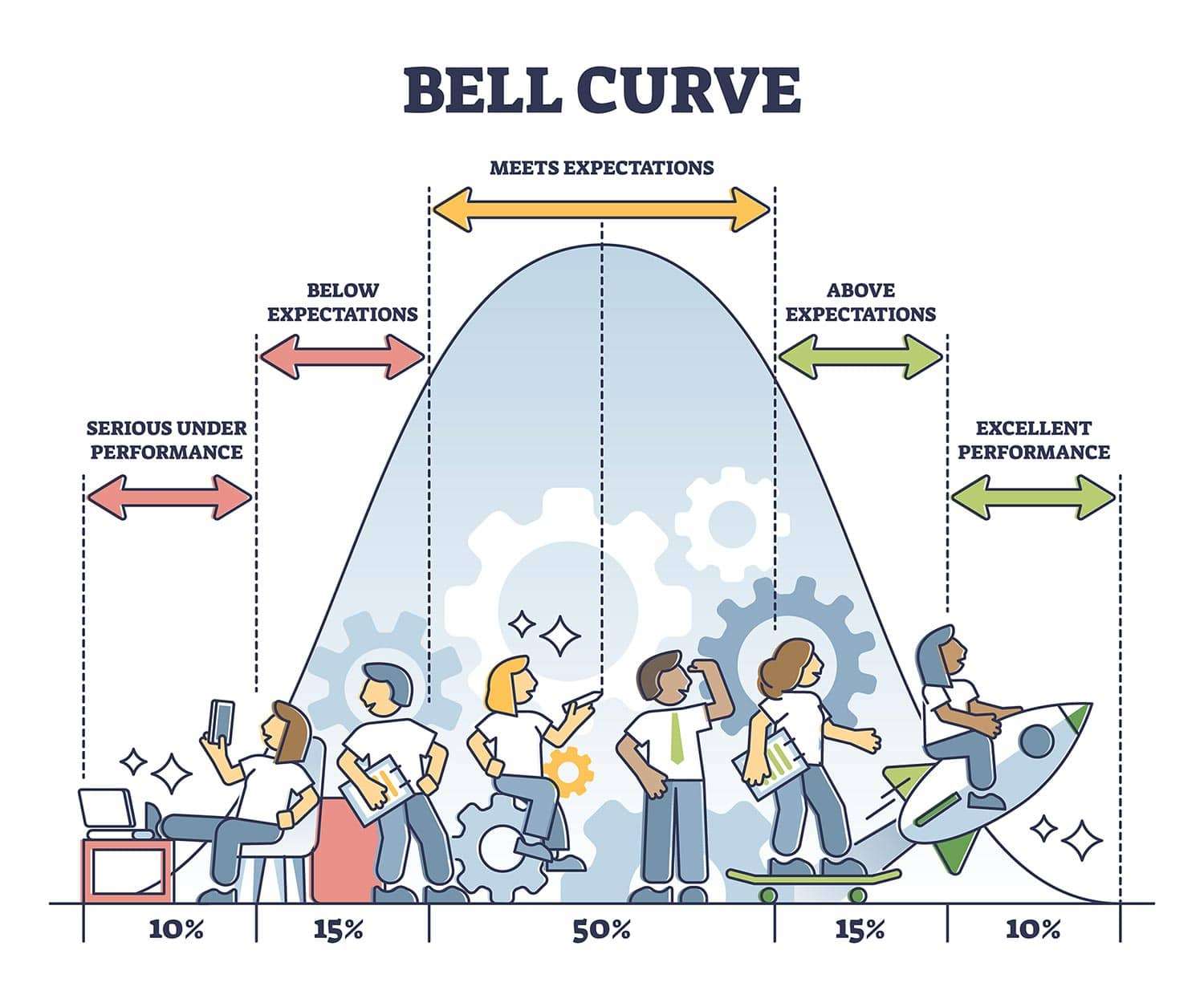
توزیع نرمال (منحنی زنگوله ای)

منحنی زنگوله‌ای شکل، که با نام‌های توزیع نرمال یا توزیع گاوسی نیز شناخته می‌شود، یک توزیع احتمال متقارن در آمار است. این منحنی نموداری را نشان می‌دهد که در آن داده‌ها در اطراف میانگین، با بیشترین فراوانی در مرکز، خوشه‌بندی می‌شوند و به تدریج به سمت دنباله‌ها کاهش می‌یابند.

ویژگی‌های توزیع نرمال

توزیع نرمال یک توزیع احتمال پیوسته است که در دو طرف میانگین متقارن است، بنابراین سمت راست مرکز، تصویر آینه‌ای سمت چپ است.

مساحت زیر منحنی توزیع نرمال نشان دهنده احتمال است و مجموع مساحت کل زیر منحنی برابر با یک است.

بیشتر مقادیر داده‌های پیوسته در توزیع نرمال تمایل دارند در اطراف میانگین جمع شوند و هرچه یک مقدار از میانگین دورتر باشد، احتمال وقوع آن کمتر است.

دم‌ها مجانبی (asymptotic) هستند، به این معنی که به افق (یعنی محور x) نزدیک می‌شوند اما هرگز کاملاً به آن نمی‌رسند.

برای یک توزیع کاملاً نرمال، میانگین، میانه و مد یک مقدار خواهند بود که به صورت بصری با قله منحنی نشان داده می‌شود.

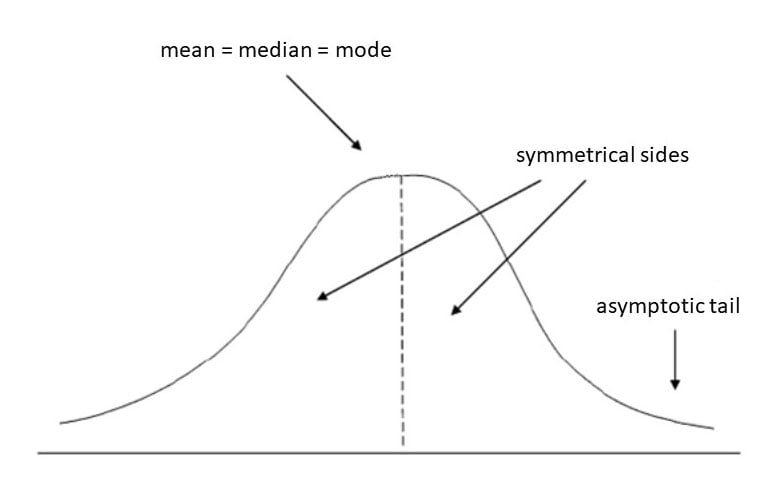
توزیع نرمال اغلب منحنی زنگوله‌ای نامیده می‌شود زیرا نمودار چگالی احتمال آن شبیه زنگوله است. همچنین به نام توزیع گاوسی نیز شناخته می‌شود، به افتخار ریاضیدان آلمانی کارل گاوس که اولین بار آن را توصیف کرد.

توزیع نرمال در مقابل توزیع نرمال استاندارد؟

توزیع نرمال با دو پارامتر میانگین و واریانس تعیین می‌شود. توزیع نرمال با میانگین ۰ و انحراف معیار ۱، توزیع نرمال استاندارد نامیده می‌شود.

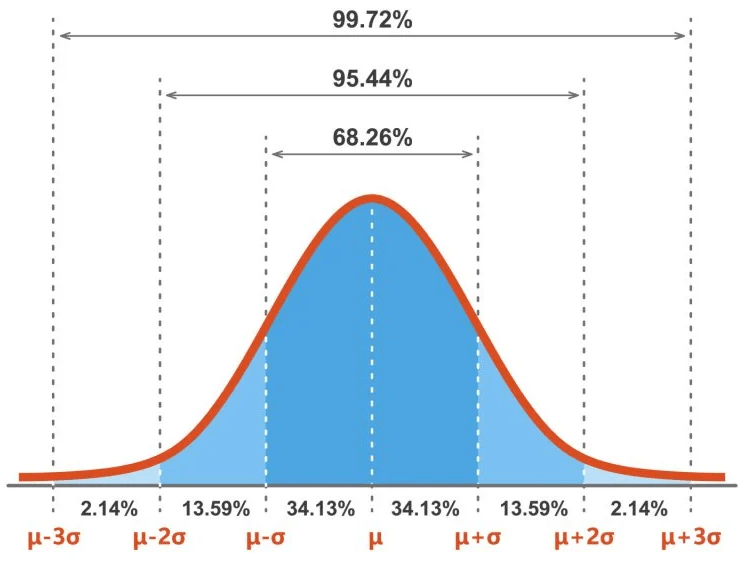
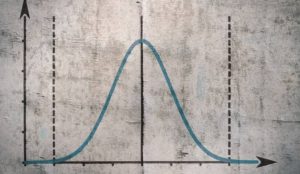
شکل ۱. توزیع نرمال استاندارد (SND).

این توزیعی است که برای ساخت جداول توزیع نرمال استفاده می‌شود.

چرا توزیع نرمال مهم است؟

منحنی زنگوله‌ای شکل یک ویژگی مشترک در طبیعت و روانشناسی است.

توزیع نرمال مهمترین توزیع احتمال در آمار است زیرا بسیاری از داده‌های پیوسته در طبیعت و روانشناسی این منحنی زنگوله‌ای شکل را هنگام گردآوری و رسم نمودار نشان می‌دهند.

به عنوان مثال، اگر به طور تصادفی ۱۰۰ نفر را نمونه‌گیری کنیم، انتظار داریم منحنی فراوانی توزیع نرمال را برای بسیاری از متغیرهای پیوسته مانند ضریب هوشی، قد، وزن و فشار خون ببینیم.

آزمون‌های پارامتری معناداری نیاز به توزیع نرمال نقاط داده نمونه دارند.

قدرتمندترین آزمون‌های آماری (پارامتری) که روانشناسان استفاده می‌کنند، نیاز به توزیع نرمال داده‌ها دارند.

اگر داده‌ها شبیه منحنی زنگوله‌ای نباشند، محققان ممکن است از یک آزمون آماری کم‌قدرت‌تر به نام آمار غیرپارامتری استفاده کنند.

تبدیل نمرات خام یک توزیع نرمال به نمرات z

ما می‌توانیم مقادیر توزیع نرمال (نمرات خام) را با تبدیل آنها به نمرات z استاندارد کنیم.

این روش به محققان اجازه می‌دهد تا نسبت مقادیری را که در تعداد مشخصی از انحراف معیار از میانگین قرار می‌گیرند، تعیین کنند (یعنی، قانون تجربی را محاسبه کنند).

فرمول قانون تجربی چیست؟

قانون تجربی در آمار به محققان اجازه می‌دهد تا نسبت مقادیری را که در فواصل مشخصی از میانگین قرار می‌گیرند، تعیین کنند.

قانون تجربی اغلب به عنوان قانون سه سیگما یا قانون 68-95-99.7 شناخته می‌شود.

اگر مقادیر داده‌ها در یک توزیع نرمال به نمره استاندارد (نمره z) در یک توزیع نرمال استاندارد تبدیل شوند، قانون تجربی درصد داده‌هایی را که در تعداد مشخصی از انحراف معیار (σ) از میانگین (μ) برای منحنی‌های زنگوله‌ای شکل قرار می‌گیرند، توصیف می‌کند.

این قانون تجربی به محققان اجازه می‌دهد تا احتمال به دست آوردن تصادفی یک نمره از یک توزیع نرمال را محاسبه کنند.

۶۸٪ از داده‌ها در اولین انحراف معیار از میانگین قرار می‌گیرند. این بدان معناست که ۶۸٪ احتمال انتخاب تصادفی یک نمره بین انحراف معیار -۱ و +۱ از میانگین وجود دارد.

۹۵٪ از مقادیر در فاصله دو انحراف معیار از میانگین قرار می‌گیرند. این بدان معناست که احتمال ۹۵٪ برای انتخاب تصادفی نمره‌ای بین -۲ و +۲ انحراف معیار از میانگین وجود دارد.

۹۹.۷٪ از داده‌ها در محدوده سه انحراف معیار از میانگین قرار می‌گیرند. این بدان معناست که احتمال ۹۹.۷٪ برای انتخاب تصادفی نمره‌ای بین -۳ و +۳ انحراف معیار از میانگین وجود دارد.

نحوه بررسی داده‌ها

با محاسبه سه معیار گرایش مرکزی، می‌توان از نرم‌افزارهای آماری (مانند SPSS) برای بررسی توزیع نرمال مجموعه داده‌های خود استفاده کرد.

اگر میانگین، میانه و مد مقادیر بسیار مشابهی داشته باشند، احتمال زیادی وجود دارد که داده‌ها از توزیع زنگوله‌ای شکل پیروی کنند (دستور SPSS در اینجا).

همچنین توصیه می‌شود از نمودار فراوانی نیز استفاده کنید تا بتوانید شکل بصری داده‌های خود را بررسی کنید (اگر نمودار شما هیستوگرام است، می‌توانید با استفاده از SPSS یک منحنی توزیع اضافه کنید: از منوها، گزینه Elements > Show Distribution Curve را انتخاب کنید).

هرچه سطح اندازه‌گیری دقیق‌تر و نمونه از یک جمعیت بزرگتر باشد، توزیع‌های نرمال آشکارتر (یعنی بی‌نقص‌تر) می‌شوند.

همچنین می‌توانید ضرایبی را محاسبه کنید که در مورد اندازه دنباله‌های توزیع در رابطه با برآمدگی در وسط منحنی زنگوله‌ای به ما می‌گویند.

به عنوان مثال، آزمون‌های کولموگروف اسمیرنوف و شاپیرو-ویلک را می‌توان با استفاده از SPSS محاسبه کرد.

این آزمون‌ها داده‌های شما را با توزیع نرمال مقایسه می‌کنند و یک مقدار p ارائه می‌دهند که اگر معنی‌دار باشد (p < 0.05)، نشان می‌دهد که داده‌های شما با توزیع نرمال متفاوت است (بنابراین، در این مورد، ما نتیجه معنی‌دار نمی‌خواهیم و به مقدار p بالاتر از 0.05 نیاز داریم).

مطالب مرتبط مفید

آزمون کولموگروف- اسمیرنوف

آزمون شاپیرو-ویلک (Shapiro-Wilk test)

آزمون نرمال بودن داده ها (Normality Test)