تحلیل رگرسیون
رگرسیون چیست؟
تحلیل رگرسیون امکان بررسی رابطه بین متغیرها را فراهم میکند. معمولاً متغیرها به صورت وابسته یا مستقل برچسبگذاری میشوند. متغیر مستقل، ورودی، محرک یا عاملی است که بر متغیر وابسته (که میتوان آن را پیامد نیز نامید) تأثیر میگذارد. به عنوان مثال، اگر بگوییم سن بر عملکرد تحصیلی دانشآموزان تأثیر میگذارد، متغیرهای مستقل و وابسته در اینجا چه خواهند بود؟ خب، در اینجا سن یک متغیر مستقل است و پتانسیل تأثیر بر متغیر پیامد/وابسته – در این مورد، عملکرد تحصیلی – را دارد. به طور مشابه، در مثال مربی پرستاری، تفکر انتقادی یک متغیر وابسته و سن، تجربه و آموزش متغیرهای مستقل هستند.
اهداف تحلیل رگرسیون
تحلیل رگرسیون چهار هدف اصلی دارد: توصیف، تخمین، پیشبینی و کنترل. رگرسیون میتواند رابطه بین متغیرهای وابسته و مستقل را توضیح دهد. تخمین به این معنی است که با استفاده از مقادیر مشاهده شده متغیرهای مستقل، میتوان مقدار متغیر وابسته را تخمین زد. تحلیل رگرسیون میتواند برای پیشبینی پیامدها و تغییرات در متغیرهای وابسته بر اساس روابط متغیرهای وابسته و مستقل مفید باشد. در نهایت، رگرسیون امکان کنترل تأثیر یک یا چند متغیر مستقل را در حین بررسی رابطه یک متغیر مستقل با متغیر وابسته فراهم میکند.
انواع تحلیل رگرسیون
معمولاً سه نوع تحلیل رگرسیون وجود دارد، یعنی رگرسیون خطی، لجستیک و چندگانه. تفاوتهای بین این انواع در جدول 1 از نظر هدف، ماهیت متغیرهای وابسته و مستقل، فرضیات اساسی و ماهیت منحنی بیان شده است. با این حال، بحث مفصلتر در مورد رگرسیون خطی به شرح زیر ارائه شده است.
جدول 1. مقایسه رگرسیون خطی، لجستیک و چندگانه
| رگرسیون خطی | رگرسیون لجستیک | رگرسیون چندگانه |
|---|---|---|
| هدف | ||
| رابطه بین یک متغیر مستقل با یک متغیر وابسته پیوسته را بررسی میکند | احتمال رویداد را با نتیجه دودویی (یعنی بله یا خیر) محاسبه میکند. | این مدل، بسطی از رگرسیون خطی ساده است و رابطه بین یک یا چند متغیر مستقل و وابسته را به طور همزمان بررسی میکند. |
| ماهیت متغیرهای وابسته و مستقل | ||
| متغیر وابسته باید پیوسته باشد.
متغیرهای مستقل میتوانند در هر سطح اندازهگیری باشند. |
متغیر وابسته باید مقولهای (Categorical) باشد.
متغیرهای مستقل میتوانند در هر سطح اندازهگیری باشند. |
متغیرهای وابسته باید پیوسته باشند.
متغیرهای مستقل میتوانند در هر سطح اندازهگیری باشند. |
| فرضیات | ||
| فرض میکند که توزیع دادههای وابسته نرمال یا گاوسی است.
نیاز به یک رابطه خطی بین متغیرهای وابسته و مستقل دارد. |
فرض میکند که توزیع دادههای وابسته دوجملهای (binomial) است.
نیازی به رابطه خطی بین متغیرهای وابسته و مستقل ندارد. متغیرهای مستقل نباید با هم همبستگی داشته باشند. |
فرض میکند که توزیع دادههای وابسته نرمال یا گاوسی است.
نیاز به یک رابطه خطی بین متغیرهای وابسته و مستقل دارد. متغیرهای مستقل نباید با هم همبستگی داشته باشند. همبستگی بالاتر بین متغیرهای مستقل ممکن است بر رابطه بین متغیر مستقل و وابسته تأثیر بگذارد. |
| ماهیت منحنی | ||
| از خط مستقیم استفاده میکند | از منحنی S شکل استفاده میکند | از خط مستقیم استفاده میکند |
| مثال | ||
| بررسی رابطه بین ساعات آموزش و سطوح مراقبت از خود بیمار و پیشبینی اینکه آموزش برای هر واحد افزایش در سطوح مراقبت از خود چقدر باید طول بکشد | تخمین احتمال ایجاد زخمهای فشاری (پیامد دوگانه: بله یا خیر) به دلیل مدت طولانیتر بستری در بیمارستان، تعداد دفعات قرارگیری در وضعیت مناسب، BMI (شاخص توده بدنی) و سن | بررسی رابطه بین ساعات آموزش و سطح مراقبت از خود بیمار ضمن کنترل سایر متغیرها (مانند حمایت خانواده، مدت زمان بیماری) که ممکن است بر این رابطه تأثیر بگذارند |
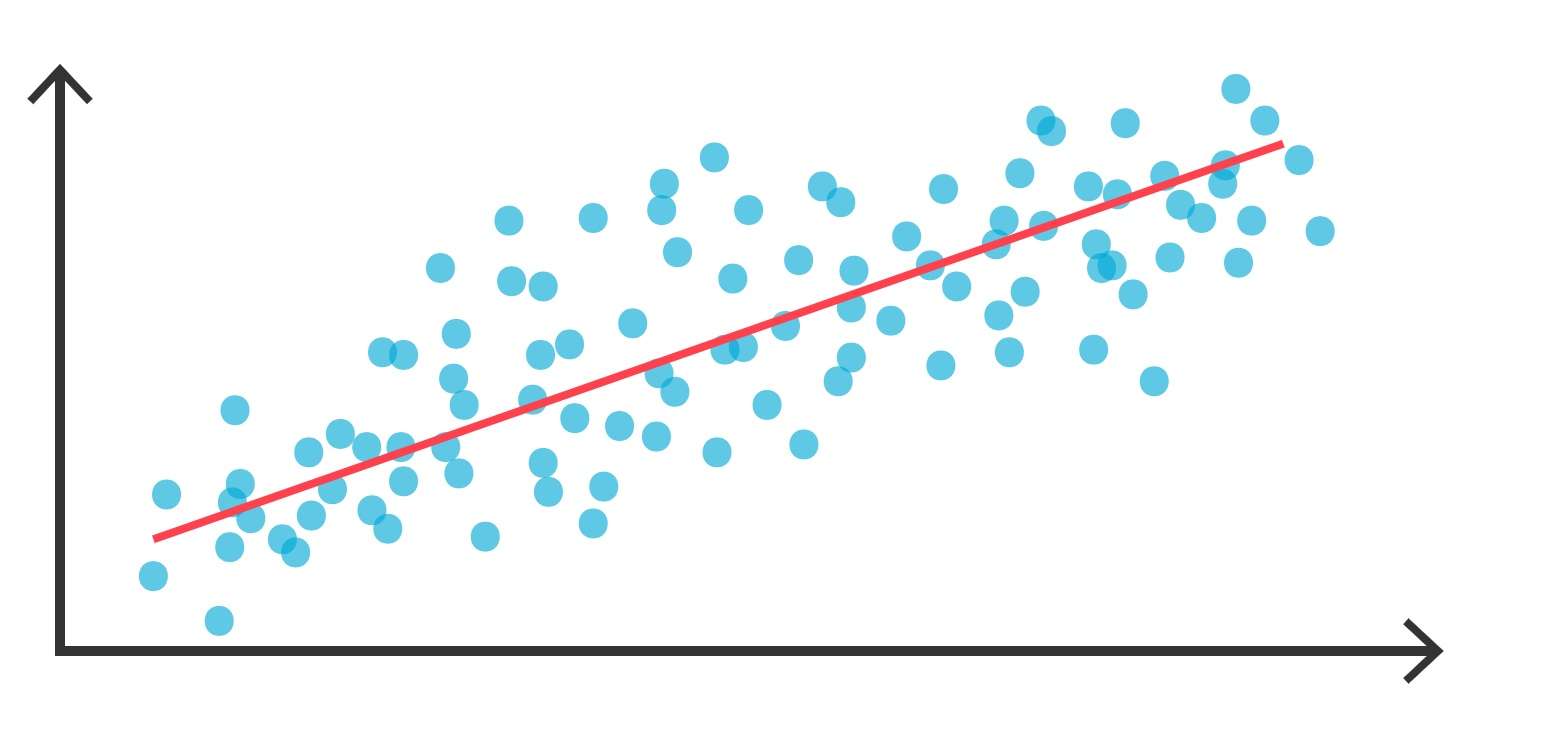
رگرسیون خطی و تفسیر
تحلیل رگرسیون خطی شامل بررسی رابطه بین یک متغیر مستقل و وابسته است. از نظر آماری، رابطه بین یک متغیر مستقل (x) و یک متغیر وابسته (y) به صورت زیر بیان میشود: y= β0+ β1x+ε. در این معادله، β0 عرض از مبدا y است و به مقدار تخمینی y اشاره دارد وقتی x برابر با 0 باشد. ضریب β1 ضریب رگرسیون است و نشان میدهد که افزایش تخمینی در متغیر وابسته برای هر واحد افزایش در متغیر مستقل چقدر است. نماد ε یک جزء خطای تصادفی است و نشاندهنده عدم دقت رگرسیون است که نشان میدهد در عمل واقعی، متغیرهای مستقل نمیتوانند تغییر در هیچ متغیر وابستهای را به طور کامل پیشبینی کنند.1 رگرسیون خطی چندگانه از همان منطق رگرسیون خطی تک متغیره پیروی میکند، با این تفاوت که (الف) رگرسیون چندگانه، بیش از یک متغیر مستقل وجود دارد و (ب) باید عدم همخطی بین متغیرهای مستقل وجود داشته باشد.
عوامل مؤثر بر رگرسیون
تحلیلهای رگرسیون خطی و چندگانه تحت تأثیر عواملی مانند اندازه نمونه، دادههای از دست رفته و ماهیت نمونه قرار میگیرند.
- اندازه نمونه کوچک ممکن است فقط ارتباط بین متغیرهایی با رابطه قوی را نشان دهد. بنابراین، اندازه نمونه باید بر اساس تعداد متغیرهای مستقل و با توجه به قدرت رابطه انتخاب شود.
- مقادیر از دست رفته زیاد در مجموعه دادهها ممکن است بر اندازه نمونه تأثیر بگذارند. بنابراین، قبل از انجام تحلیلهای رگرسیون، باید به طور مناسب به همه مقادیر از دست رفته رسیدگی شود.
- زیرنمونههای درون نمونه بزرگتر ممکن است اثر واقعی متغیرهای مستقل و وابسته را پنهان کنند. بنابراین، اگر زیرنمونهها از پیش تعریف شده باشند، میتوان از رگرسیون درون نمونه برای تشخیص روابط واقعی استفاده کرد. در غیر این صورت، تحلیل باید روی کل نمونه انجام شود.
چه زمانی باید از تحلیل رگرسیون استفاده کنم؟
از تحلیل رگرسیون برای توصیف روابط بین مجموعهای از متغیرهای مستقل و متغیر وابسته استفاده کنید. تحلیل رگرسیون یک معادله رگرسیون تولید میکند که در آن ضرایب، رابطه بین هر متغیر مستقل و متغیر وابسته را نشان میدهند. همچنین میتوانید از این معادله برای پیشبینی استفاده کنید.
تحلیل رگرسیون میتواند کارهای زیادی را انجام دهد. برای مثال، میتوانید از تحلیل رگرسیون برای انجام موارد زیر استفاده کنید:
- مدلسازی چندین متغیر مستقل
- شامل متغیرهای پیوسته و دستهبندیشده
- استفاده از عبارات چندجملهای برای مدلسازی انحنا
- ارزیابی عبارات تعاملی برای تعیین اینکه آیا اثر یک متغیر مستقل به مقدار متغیر دیگر بستگی دارد یا خیر
این قابلیتها همگی جالب هستند، اما شامل یک توانایی تقریباً جادویی نمیشوند. تحلیل رگرسیون میتواند مسائل بسیار پیچیدهای را که متغیرها مانند اسپاگتی در هم تنیدهاند، حل کند. برای مثال، تصور کنید که شما محققی هستید که هر یک از موارد زیر را مطالعه میکنید:
- آیا وضعیت اجتماعی-اقتصادی و نژاد بر پیشرفت تحصیلی تأثیر میگذارند؟
- آیا تحصیلات و بهره هوشی بر درآمد تأثیر میگذارند؟
- آیا عادات ورزشی و رژیم غذایی بر وزن تأثیر میگذارند؟
- آیا نوشیدن قهوه و سیگار کشیدن با خطر مرگ و میر مرتبط است؟
- آیا یک مداخله ورزشی خاص بر تراکم استخوان تأثیری دارد که متمایز از سایر فعالیتهای بدنی است؟
همه این سوالات تحقیقاتی متغیرهای مستقلی را در خود جای دادهاند که میتوانند بر متغیرهای وابسته تأثیر بگذارند. چگونه میتوان شبکهای از متغیرهای مرتبط را از هم جدا کرد؟ کدام متغیرها از نظر آماری معنادار هستند و هر کدام چه نقشی ایفا میکنند؟ رگرسیون به کمک میآید زیرا میتوانید از آن برای همه این سناریوها استفاده کنید!
استفاده از تحلیل رگرسیون برای کنترل متغیرهای مستقل
همانطور که اشاره کردم، تحلیل رگرسیون نحوه ارتباط تغییرات در هر متغیر مستقل با تغییرات در متغیر وابسته را شرح میدهد. از همه مهمتر، رگرسیون از نظر آماری هر متغیر را در مدل شما کنترل میکند.
کنترل یک متغیر به چه معناست؟
هنگامی که تحلیل رگرسیون را انجام میدهید، باید نقش هر متغیر را جدا کنید. به عنوان مثال، من در یک مطالعه مداخله ورزشی شرکت کردم که هدف ما تعیین این بود که آیا مداخله، تراکم مواد معدنی استخوان افراد را افزایش داده است یا خیر. ما باید نقش مداخله ورزشی را از هر چیز دیگری که میتواند بر تراکم مواد معدنی استخوان تأثیر بگذارد، از رژیم غذایی گرفته تا سایر فعالیتهای بدنی، جدا میکردیم.
برای رسیدن به این هدف، باید اثر متغیرهای مخدوشکننده را به حداقل برسانید. تحلیل رگرسیون این کار را با تخمین تأثیر تغییر یک متغیر مستقل بر متغیر وابسته در حالی که سایر متغیرهای مستقل ثابت نگه داشته میشوند، انجام میدهد. این فرآیند به شما امکان میدهد نقش هر متغیر مستقل را بدون نگرانی در مورد سایر متغیرهای موجود در مدل بیاموزید. باز هم، شما میخواهید اثر هر متغیر را جدا کنید.
مدلهای رگرسیون با کنترل متغیرهای مخدوشکننده به شما کمک میکنند تا از گیج شدن نتایج توسط همبستگیهای کاذب جلوگیری کنید.
چگونه سایر متغیرها را در رگرسیون کنترل میکنید؟
یکی از جنبههای زیبای تحلیل رگرسیون این است که شما سایر متغیرهای مستقل را صرفاً با گنجاندن آنها در مدل خود ثابت نگه میدارید! بیایید این موضوع را در عمل با یک مثال بررسی کنیم.
یک مطالعه اخیر، تأثیر مصرف قهوه بر مرگ و میر را تجزیه و تحلیل کرد. نتایج اولیه نشان داد که مصرف بیشتر قهوه با خطر بالاتر مرگ مرتبط است. با این حال، مصرفکنندگان قهوه اغلب سیگار میکشند و محققان سیگار کشیدن را در مدل اولیه خود لحاظ نکردند. پس از اینکه سیگار کشیدن را در مدل لحاظ کردند، نتایج رگرسیون نشان داد که مصرف قهوه خطر مرگ و میر را کاهش میدهد در حالی که سیگار کشیدن آن را افزایش میدهد. این مدل نقش هر متغیر را در حالی که متغیر دیگر ثابت نگه داشته میشود، جدا میکند. میتوانید ضمن کنترل سیگار کشیدن، تأثیر مصرف قهوه را ارزیابی کنید. به راحتی، هنگام بررسی تأثیر سیگار کشیدن، مصرف قهوه را نیز کنترل میکنید.
توجه داشته باشید که این مطالعه همچنین نشان میدهد که چگونه حذف یک متغیر مرتبط میتواند نتایج گمراهکنندهای ایجاد کند. حذف یک متغیر مهم باعث میشود که کنترل نشده باشد و میتواند نتایج متغیرهایی را که در مدل لحاظ میکنید، دچار سوگیری کند. این هشدار به ویژه برای مطالعات مشاهدهای که در آنها اثرات متغیرهای حذف شده ممکن است نامتعادل باشد، کاربرد دارد. از سوی دیگر، فرآیند تصادفیسازی در یک آزمایش واقعی تمایل دارد اثرات این متغیرها را به طور مساوی توزیع کند، که این امر سوگیری متغیر حذف شده را کاهش میدهد.
نحوه تفسیر خروجی رگرسیون
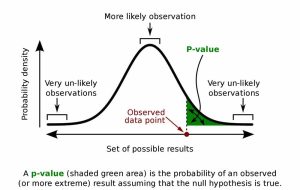
برای پاسخ به سوالات با استفاده از تحلیل رگرسیون، ابتدا باید مدل را برازش داده و تأیید کنید که مدل خوبی دارید. سپس، ضرایب رگرسیون و مقادیر p را بررسی میکنید. وقتی مقدار p پایینی دارید (معمولاً < 0.05)، متغیر مستقل از نظر آماری معنادار است. ضرایب نشان دهنده میانگین تغییر در متغیر وابسته با توجه به تغییر یک واحدی در متغیر مستقل (IV) در حالی که سایر متغیرهای مستقل را کنترل میکنید، هستند.
به عنوان مثال، اگر متغیر وابسته شما درآمد باشد و متغیرهای مستقل شما شامل ضریب هوشی و تحصیلات (از جمله سایر متغیرهای مرتبط) باشند، ممکن است خروجی مانند این را مشاهده کنید:

مقادیر p پایین نشان میدهد که هم تحصیلات و هم ضریب هوشی از نظر آماری معنادار هستند. ضریب ضریب هوشی نشان میدهد که هر امتیاز اضافی ضریب هوشی، درآمد شما را به طور متوسط تقریباً 4.80 دلار افزایش میدهد، در حالی که سایر متغیرها در مدل کنترل میشوند. علاوه بر این، یک واحد اضافی تحصیلات، میانگین درآمد را 24.22 دلار افزایش میدهد، در حالی که سایر متغیرها ثابت نگه داشته میشوند.
تحلیل رگرسیون نوعی آمار استنباطی است. مقادیر p به تعیین اینکه آیا روابطی که در نمونه خود مشاهده میکنید، در جمعیت بزرگتر نیز وجود دارد یا خیر، کمک میکند. من یک پست وبلاگ کامل در مورد نحوه تفسیر ضرایب رگرسیون و مقادیر p آنها نوشتهام که اکیداً توصیه میکنم.
به دست آوردن نتایج رگرسیون قابل اعتماد
با قدرت گسترده استفاده از رگرسیون، مسئولیت بزرگی نیز به همراه دارد. متاسفیم، اما باید اینطور باشد. برای به دست آوردن نتایج رگرسیونی که بتوانید به آنها اعتماد کنید، باید موارد زیر را انجام دهید:
مدل صحیح را مشخص کنید. همانطور که دیدیم، اگر نتوانید تمام متغیرهای مهم را در مدل خود بگنجانید، نتایج میتوانند سوگیری داشته باشند.
نمودارهای باقیمانده خود را بررسی کنید. مطمئن شوید که مدل شما به اندازه کافی با دادهها برازش دارد. همبستگی بین متغیرهای مستقل، همخطی چندگانه نامیده میشود. همانطور که دیدیم، مقداری همخطی چندگانه قابل قبول است. با این حال، همخطی چندگانه بیش از حد میتواند مشکلساز باشد.
استفاده از تحلیل رگرسیون به شما این امکان را میدهد که اثرات سوالات پیچیده تحقیقاتی را از هم جدا کنید. میتوانید با مدلسازی و کنترل تمام متغیرهای مرتبط، رشتههای اسپاگتی را از هم جدا کنید و سپس نقشی را که هر یک ایفا میکنند ارزیابی کنید.




پاسخگوی سوالات و نظرات شما هستیم