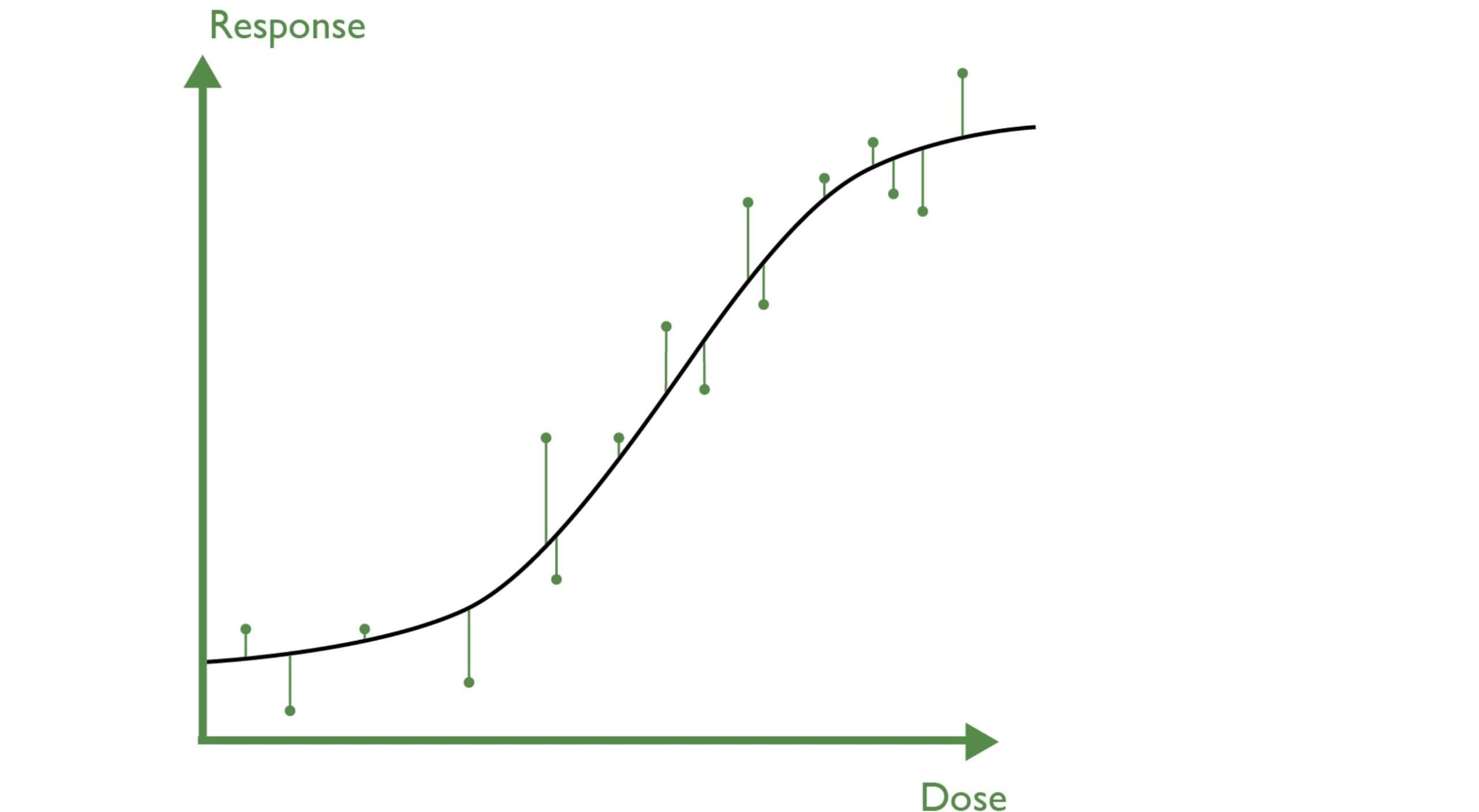
نیکویی برازش

نیکویی برازش چیست؟

نیکویی برازش، میزان تطابق داده‌های مشاهده‌شده با مقادیر مورد انتظار از یک مدل آماری را ارزیابی می‌کند.

وقتی وارد بحث آمار می‌شوید، اغلب می‌پرسید: «مدل من چقدر با داده‌ها برازش دارد؟» اگر برازش قوی باشد، مدل شما عالی است. اگر برازش سست باشد؟ شاید بهتر باشد در مورد آن مدل تجدید نظر کنید. این ماهیت نیکویی برازش است. به طور خاص:

• نیکویی برازش بالا نشان می‌دهد که مقادیر مشاهده شده نزدیک به مقادیر مورد انتظار مدل هستند.
• نیکویی برازش پایین نشان می‌دهد که مقادیر مشاهده شده نسبتاً از مقادیر مورد انتظار فاصله دارند.

مدلی که به خوبی با داده‌ها برازش داشته باشد، پیش‌بینی‌های دقیق و بینش‌های عمیق‌تری ارائه می‌دهد، در حالی که برازش ضعیف می‌تواند منجر به نتیجه‌گیری‌ها و پیش‌بینی‌های گمراه‌کننده شود. اطمینان از برازش خوب برای نتایج قابل اعتماد و اقدامات آگاهانه بسیار مهم است.

معیار نیکویی برازش، اندازه تفاوت‌های بین داده‌های مشاهده شده و مقادیر مورد انتظار مدل را خلاصه می‌کند. آزمون نیکویی برازش تعیین می‌کند که آیا تفاوت‌ها از نظر آماری معنادار هستند یا خیر. علاوه بر این، آنها می‌توانند ما را در انتخاب مدلی که نمایش بهتری ارائه می‌دهد، راهنمایی کنند. معیار و آزمون نیکویی برازش مناسب به شرایط بستگی دارد.

در این پست سایت، شما با مفهوم نیکویی برازش در زمینه‌های حیاتی مدل‌های رگرسیون و توزیع‌های احتمال آشنا خواهید شد. ما آن را در مدل‌های رگرسیون اندازه‌گیری خواهیم کرد و یاد خواهیم گرفت که چگونه داده‌های نمونه را با استفاده از آزمون‌های نیکویی برازش در برابر توزیع‌ها آزمایش کنیم.

نیکویی برازش در مدل‌های رگرسیون

در مدل‌های رگرسیون، درک نیکویی برازش برای اطمینان از پیش‌بینی‌های دقیق و بینش‌های معنادار بسیار مهم است. در اینجا، به معیارهای کلیدی که این همسویی را با داده‌ها نشان می‌دهند، خواهیم پرداخت.

یک مدل رگرسیون زمانی به خوبی بر داده‌ها برازش می‌دهد که تفاوت بین مقادیر مشاهده شده و پیش‌بینی شده کوچک و بی‌طرفانه باشد. آمارشناسان به این تفاوت‌ها به عنوان باقیمانده‌ها اشاره می‌کنند.

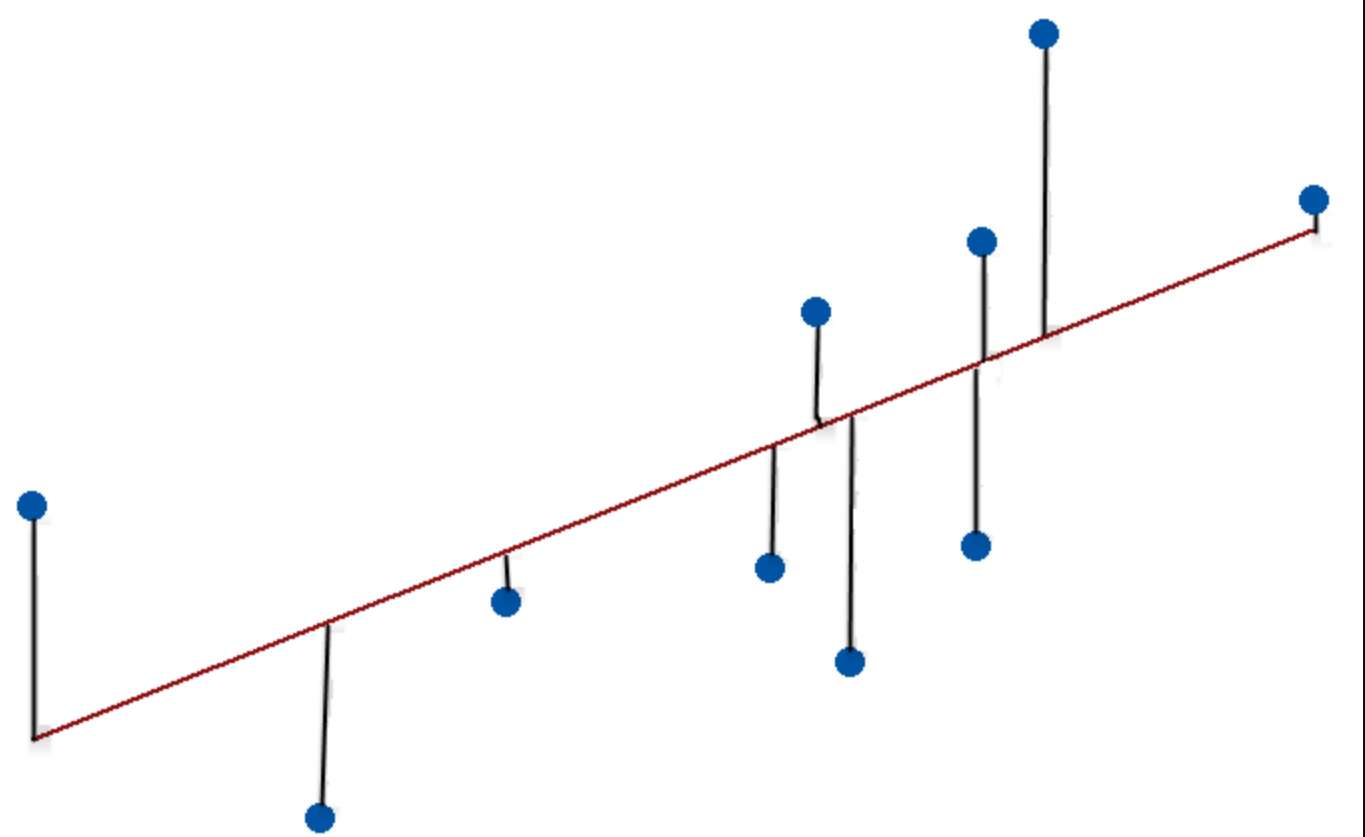
با افزایش نیکویی برازش، نقاط داده به خط برازش شده مدل نزدیک‌تر می‌شوند.

ضریب تعیین (R²)

ضریب تعیین (R²) یک آماره نیکویی برازش برای مدل‌های رگرسیون خطی است. این شاخص، درصد تغییرات متغیر وابسته‌ای را که مدل توضیح می‌دهد، با استفاده از مقیاس مناسب ۰ تا ۱۰۰٪ اندازه‌گیری می‌کند.

ضریب تعیین (R-squared) پراکندگی داده‌ها را در اطراف خط رگرسیون برازش شده ارزیابی می‌کند. برای یک مجموعه داده، مقادیر بالاتر ضریب تعیین (R-squared) نشان‌دهنده تفاوت‌های کمتر بین داده‌های نمونه و مقادیر برازش شده است.

مدلی که پراکندگی بیشتری دارد، ضریب تعیین (R-square) برابر با ۱۵٪ دارد، در حالی که مدلی که پراکندگی کمتری دارد، ۸۵٪ است.

R² را به عنوان درصدی در نظر بگیرید که تغییرات را توضیح می‌دهد. R² بالاتر؟ پس برازش بهتری دارد.

• R² بالا: مدل شما تغییرات زیادی را در بر می‌گیرد.
• R² پایین: مدل بخش زیادی از واریانس را توضیح نمی‌دهد.

به یاد داشته باشید، این تنها شاخص نیست. R² بالا همیشه به معنای یک مدل بی‌نقص نیست!

خطای استاندارد رگرسیون (S)

این خطای استاندارد رگرسیون، معیار خوبی برای برازش است که اندازه معمول اختلاف مطلق بین مقادیر مشاهده شده و پیش‌بینی شده را ارائه می‌دهد. S از واحدهای متغیر وابسته (DV) استفاده می‌کند.

• S کوچک: پیش‌بینی‌ها به مقادیر داده‌ها نزدیک هستند.
• S بزرگ: پیش‌بینی‌ها انحراف بیشتری دارند.

فرض کنید مدل شما از شاخص توده بدنی (BMI) برای پیش‌بینی درصد چربی بدن (DV) استفاده می‌کند. در نتیجه، اگر S مدل شما 3.5 باشد، می‌دانید که مقادیر پیش‌بینی شده آن معمولاً 3.5٪ از مقادیر درصد چربی بدن مشاهده شده است.

با این حال، آن را به صورت جداگانه در نظر نگیرید. برای درک بهتر، آن را با واحدهای متغیر وابسته مقایسه کنید.

معیار اطلاعات آکایک (AIC)

معیار اطلاعات آکایک (AIC) یک معیار نیکویی برازش است که آماردانان برای مقایسه مدل‌ها و کمک به شما در انتخاب بهترین مدل طراحی کرده‌اند. مقدار AIC به خودی خود معنادار نیست، اما شما به دنبال مدلی با کمترین AIC هستید.

• AIC پایین‌تر: مدل شما احتمالاً بهتر است (هنگام مقایسه).
• تنظیم پیچیدگی: مدل‌های ساده‌تر وقتی برازش خوبی دارند، ترجیح داده می‌شوند.

یاد بگیرید که چرا یک مدل ساده‌تر می‌خواهید، که آماردانان آن را مدل پارسیمونیوس می‌نامند: در رابطه با مدل پارسیمونیوس مطلبی خواهیم نوشت.

آمارهای نیکویی برازش دیگری مانند R² تعدیل‌شده و معیار اطلاعات بیزی (BIC) نیز وجود دارند. هر کدام قدرت منحصر به فرد خود را دارند. اما برای شروع، روی این سه مورد تمرکز کنید.

نیکویی برازش برای توزیع‌های احتمال

گاهی اوقات، مدل آماری شما این است که داده‌های شما از یک توزیع احتمال خاص، مانند توزیع نرمال، لگاریتمی نرمال، پواسون یا توزیع دیگری پیروی می‌کنند. شما می‌خواهید بدانید که آیا توزیع نمونه شما با توزیع فرضی سازگار است یا خیر.

چرا؟

زیرا بسیاری از آزمون‌ها و روش‌های آماری بر فرضیات توزیعی استوار هستند.

به عنوان مثال، آزمون‌های t و ANOVA فرض می‌کنند که داده‌های شما نرمال هستند. برعکس، اگر تعداد بازدیدهای روزانه از وب‌سایت را تجزیه و تحلیل می‌کنید، ممکن است انتظار توزیع پواسون را داشته باشید. تجزیه و تحلیل قابلیت در حوزه کیفیت به دانستن دقیق اینکه داده‌های شما از کدام توزیع پیروی می‌کنند، بستگی دارد.

آزمون‌های نیکویی برازش را وارد کنید.

یک آزمون نیکویی برازش تعیین می‌کند که آیا تفاوت‌های بین داده‌های نمونه شما و توزیع از نظر آماری معنادار است یا خیر. در این زمینه، معناداری آماری نشان می‌دهد که مدل به اندازه کافی با داده‌ها برازش ندارد. نتایج آزمون می‌تواند روش‌های تحلیلی مورد استفاده شما را هدایت کند.

من دو مورد از آزمون‌های نیکویی برازش موجود را پوشش خواهم داد. آزمون اندرسون-دارلینگ برای داده‌های پیوسته و آزمون نیکویی برازش کای-اسکوئر برای داده‌های دسته‌بندی‌شده و گسسته کاربرد دارد.

آزمون اندرسون-دارلینگ

آزمون نیکویی برازش اندرسون-دارلینگ، داده‌های نمونه پیوسته را با یک توزیع احتمال خاص مقایسه می‌کند. آمارشناسان اغلب از آن برای آزمون‌های نرمال بودن استفاده می‌کنند، اما آزمون اندرسون-دارلینگ می‌تواند توزیع‌های احتمال دیگری را نیز ارزیابی کند و همین امر آن را در تحلیل آماری پرکاربرد می‌کند.

فرضیه‌های آزمون اندرسون-دارلینگ به شرح زیر است:

• فرضیه صفر (H₀): داده‌ها از توزیع مشخص‌شده پیروی می‌کنند.
• فرضیه جایگزین (HA): داده‌ها از توزیع پیروی نمی‌کنند.

وقتی مقدار p کمتر از سطح معنی‌داری شما باشد، فرضیه صفر را رد کنید. در نتیجه، نتایج آماری معنادار برای آزمون نیکویی برازش نشان می‌دهد که داده‌های شما با توزیع انتخاب‌شده مطابقت ندارند و این امر مستلزم بررسی بیشتر یا تنظیمات مدل است.

تصور کنید که در حال تحقیق در مورد درصد چربی بدن دختران قبل از نوجوانی هستید و می‌خواهید بدانید که آیا این درصدها از توزیع نرمال پیروی می‌کنند یا خیر.

پس از جمع‌آوری داده‌های چربی بدن از ۹۲ دختر، آزمون اندرسون-دارلینگ را انجام می‌دهید و نتایج زیر را به دست می‌آورید.

Mean=28.57, StDev=6.989, N=92, AD=1.197, P-value<0.005

از آنجا که مقدار p کمتر از 0.05 است، فرضیه صفر را رد کنید و نتیجه بگیرید که داده‌های نمونه از توزیع نرمال پیروی نمی‌کنند.

آزمون نیکویی برازش کای دو

آزمون نیکویی برازش کای دو نشان می‌دهد که آیا نسبت‌های یک متغیر گسسته یا دسته‌بندی‌شده از توزیعی با نسبت‌های فرضی پیروی می‌کنند یا خیر.

آمارشناسان اغلب از آزمون نیکویی برازش کای دو برای ارزیابی برابری نسبت‌های پیامدهای دسته‌بندی‌شده استفاده می‌کنند. یا تحلیلگر می‌تواند نسبت‌های مورد استفاده در آزمون را فهرست کند. از طرف دیگر، این آزمون می‌تواند تعیین کند که آیا نتایج مشاهده‌شده با یک توزیع احتمال گسسته، مانند توزیع پواسون، برازش دارند یا خیر.

این آزمون نیکویی برازش موارد زیر را انجام می‌دهد:

انحرافات را محاسبه می‌کند: از اختلاف مربع بین مشاهده‌شده و مورد انتظار استفاده می‌کند.

مقدار P < 0.05: فراوانی‌های مشاهده‌شده و مورد انتظار با هم مطابقت ندارند.

تصور کنید که در مورد انصاف تاس کنجکاو هستید. شما یک تاس شش وجهی را ۶۰۰ بار پرتاب می‌کنید و انتظار دارید که اگر منصفانه باشد، هر وجه ۱۰۰ بار بیاید.

تعداد مشاهده‌شده برای ضلع‌های ۱ تا ۶ به ترتیب ۹۰، ۱۱۰، ۹۵، ۱۰۵، ۹۵ و ۱۰۵ است. مقادیر مشاهده‌شده با مقادیر مورد انتظار ۱۰۰ برای هر وجه تاس مطابقت ندارند. بیایید آزمون نیکویی برازش کای-اسکوئر را برای این داده‌ها اجرا کنیم تا ببینیم آیا این تفاوت‌ها از نظر آماری معنادار هستند یا خیر.

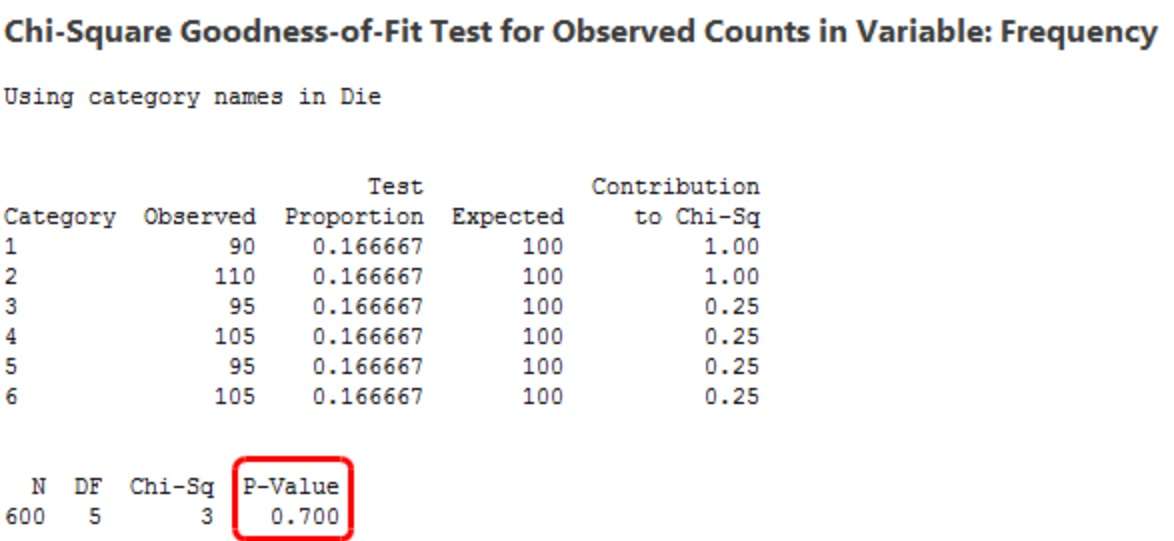
مقدار p برابر با 0.700 بزرگتر از 0.05 است، بنابراین شما نمی‌توانید فرضیه صفر را رد کنید. فراوانی‌های مشاهده شده تفاوت معناداری با فراوانی‌های مورد انتظار ندارند. داده‌های نمونه شما این ادعا را که تاس ناعادلانه است، تأیید نمی‌کند!

مطالب مرتبط مفید

فرضیه صفر یا فرض صفر

رگرسیون خطی

تحلیل رگرسیون