طرح مربع لاتین
طرح مربع لاتین چیست؟
مربع لاتین یک طرح آزمایشی است که چندین تیمار را آزمایش میکند و در عین حال دو منبع تغییرات ناخواسته، که به عنوان متغیرهای مزاحم شناخته میشوند، را کنترل میکند. این متغیرهای مزاحم عواملی هستند که شما مستقیماً آنها را مطالعه نمیکنید، اما در صورت عدم کنترل میتوانند بر نتیجه آزمایش شما تأثیر بگذارند.
مربع لاتین با مسدود کردن آنها، تأثیر متغیرهای مزاحم را کاهش میدهد. یک بلوک، گروهی از واحدهای آزمایشی است که از نظر تأثیری که محققان انتظار دارند بر نتیجه آزمایش داشته باشند، مشابه هستند. گروهبندی واحدهای مشابه به کاهش تغییرپذیری ناشی از عوامل مزاحم شناخته شده کمک میکند و تشخیص اثرات تیمار را آسانتر میکند.
در این طرحها، محققان به طور تصادفی یک واحد آزمایشی را به هر ترکیب منحصر به فرد از تیمار، بلوک ردیفی و بلوک ستونی اختصاص میدهند.
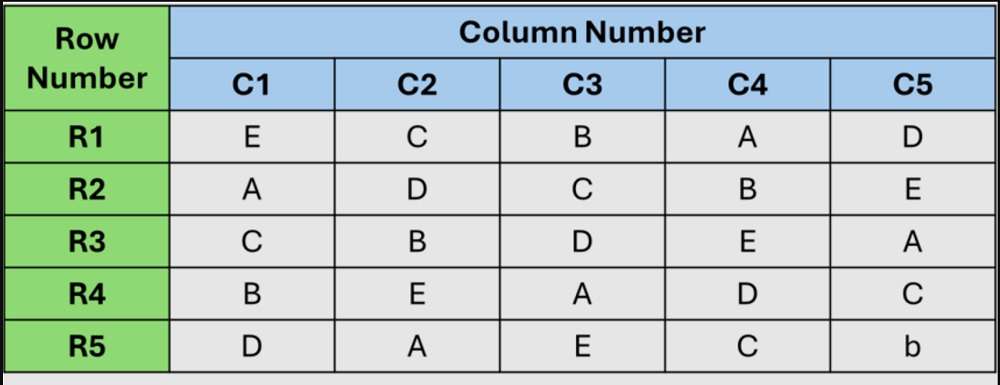
مربع لاتین یک شبکه n × n است که در آن n تعداد تیمارها و تعداد سطوح برای هر متغیر مزاحم است. تیمارها به گونهای مرتب شدهاند که هر کدام دقیقاً یک بار در هر سطر و یک بار در هر ستون ظاهر میشوند. هر سطر نشان دهنده یک بلوک برای یک متغیر مزاحم و هر ستون نشان دهنده یک بلوک برای متغیر مزاحم دیگر است. حروف موجود در شبکه نشان دهنده شرایط تیمار مختلف هستند.
ما بعداً با این مربع لاتین کار خواهیم کرد تا نحوه استفاده از آن را برای یک آزمایش نشان دهیم.
این چیدمان، درمانها یا مداخله ها را در دو متغیر مزاحم متعادل میکند و به جداسازی اثر درمان کمک میکند. این طرح، با اطمینان از اینکه هر درمان به طور مساوی در تمام سطوح هر دو متغیر مزاحم قرار میگیرد، سوگیری سیستماتیکی را که ممکن است اثرات درمان را مختل کند، از بین میبرد. این ساختار به محققان اجازه میدهد تا تفاوتهای نتیجه را با اطمینان بیشتری به درمان نسبت دهند.
چه زمانی و چرا از مربع لاتین استفاده میکنید؟
مربعهای لاتین زمانی ایدهآل هستند که میخواهید دو عامل مزاحم را به طور متعادل کنترل کنید. محققان اغلب از این طرحها در کشاورزی، روانشناسی و آزمایشهای صنعتی استفاده میکنند، به خصوص در موقعیتهایی که:
- شما تعداد محدودی واحد آزمایشی دارید.
- شما میخواهید تغییرپذیری ناشی از دو منبع خارجی شناخته شده را کنترل کنید.
- شما در حال آزمایش چندین تیمار (معمولاً ۳ تا ۶) هستید.
فرض کنید در حال آزمایش چهار نوع کود در گلخانه هستید و میخواهید نور خورشید و کیفیت خاک را مسدود کنید. یک مربع لاتین تضمین میکند که هر کود یک بار در هر سطح نور خورشید و یک بار در هر سطح کیفیت خاک ظاهر میشود.
این روش با طرحهای بلوکی تصادفی (RBD) متفاوت است. RBDها میتوانند یک یا چند عامل مزاحم را در خود جای دهند، حتی زمانی که تعداد سطوح بین عوامل مزاحم و تیمار متفاوت باشد. مربعهای لاتین روش سادهتری برای کنترل دقیقاً دو متغیر مزاحم در یک طرح متعادل ارائه میدهند.
محدودیتهای مربعهای لاتین
مربعهای لاتین نوع خاصی از طرح بلوکی هستند. اگرچه آنها با استفاده از مدلهای خطی عمومی تجزیه و تحلیل میشوند، مربعهای لاتین طرحهای فاکتوریل نیستند و نمیتوانند تعاملات را تخمین بزنند. ساختار متعامد و بسیار کنترلشده آنها، آنها را برای تنظیمات تجربی خاص مؤثر میکند.
علیرغم ظرافتشان، مربعهای لاتین الزامات سختگیرانهای دارند:
- تعداد تیمارها باید برابر با تعداد سطوح هر دو متغیر مزاحم باشد.
- هیچ تعاملی بین تیمارها و متغیرهای مزاحم وجود ندارد.
- طرح باید کامل و متعادل باشد.
این محدودیتها باعث میشود مربعهای لاتین در آزمایشهای دنیای واقعی انعطافپذیری کمتری داشته باشند. در نتیجه، محققان عمدتاً از این طرح در محیطهای کاملاً کنترلشده مانند آزمایشگاهها یا گلخانهها استفاده میکنند. در محیطهای پیچیدهتر یا نامتعادلتر، آزمایشگران اغلب از مدلهای ترکیبی خطی یا سایر طرحهای پیشرفته که میتوانند اندازه نمونهها و تعاملات نابرابر را مدیریت کنند، استفاده میکنند.
مثالی از استفاده از طرح آزمایشی مربع لاتین
فرض کنید که در حال آزمایش ۴ نوع کود (A، B، C، D) در یک آزمایش گلخانهای هستید. تیمار اصلی نوع کودی است که به گیاهان داده میشود. با این حال، شما همچنین انتظار دارید که هم میزان قرار گرفتن در معرض نور خورشید و هم کیفیت خاک میتوانند بر نتایج تأثیر بگذارند. این دو عامل، متغیرهای مزاحمی هستند که میخواهید با استفاده از طرح مربع لاتین کنترل کنید. شما سطوح نور خورشید را به عنوان بلوکهایی در ردیفها و کیفیت خاک را به عنوان بلوکهایی در ستونها در نظر خواهید گرفت.
مرحله ۱: ساخت مربع لاتین
یک مربع لاتین پایه، یک شبکه ۴×۴ است که در آن هر تیمار دقیقاً یک بار در هر سطر و دقیقاً یک بار در هر ستون ظاهر میشود. این طرح، نمایش مساوی تیمارها را در هر دو عامل مسدودکننده تضمین میکند.
روش ایدهآل برای انتخاب یک مربع لاتین برای یک آزمایش خاص، انتخاب تصادفی یکی از مجموعه کامل تمام مربعهای لاتین ممکن با اندازه مناسب است. با این حال، این میتواند از نظر محاسباتی فشرده باشد. یک رویکرد عملیتر، انتخاب تصادفی یک مربع لاتین استاندارد است – اینها مربعهای لاتینی هستند که از یک ساختار منظم و تکراری پیروی میکنند، که اغلب با تیمارها به ترتیب حروف الفبا یا عددی شروع میشوند و آنها را در ردیفها میچرخانند.
| ستون 1 | ستون 2 | ستون 3 | ستون 4 | |
| ردیف 1 | A | B | C | D |
| ردیف 2 | B | C | D | A |
| ردیف 3 | C | D | A | B |
| ردیف 4 | D | A | B | C |
مرحله ۲: اختصاص تصادفی شرایط عملیات و مسدود کردن
شرایط مسدود کردن دنیای واقعی را به صورت تصادفی به ردیفها و ستونها اختصاص دهید. در این مثال، ردیفها بلوکهایی برای سطوح قرار گرفتن در معرض نور خورشید هستند (مثلاً زیاد، متوسط-زیاد، متوسط-کم، کم). ستونها بلوکهایی برای سطوح کیفیت خاک هستند (مثلاً غنی، متوسط-غنی، متوسط-ضعیف، ضعیف). اختصاص تصادفی این سطوح از سوگیری سیستماتیک جلوگیری میکند.
سپس، محققان باید به طور تصادفی تیمارها (مثلاً انواع کود) را به حروف داخل مربع (A، B، C، D) اختصاص دهند. این کار آزمایش را بیشتر تصادفی میکند. با تصادفی کردن متغیرهای بلوکبندی و تخصیص تیمارها، طرح از تداخل ناخواسته جلوگیری میکند و تعادل لازم برای جداسازی اثرات تیمار را حفظ میکند.
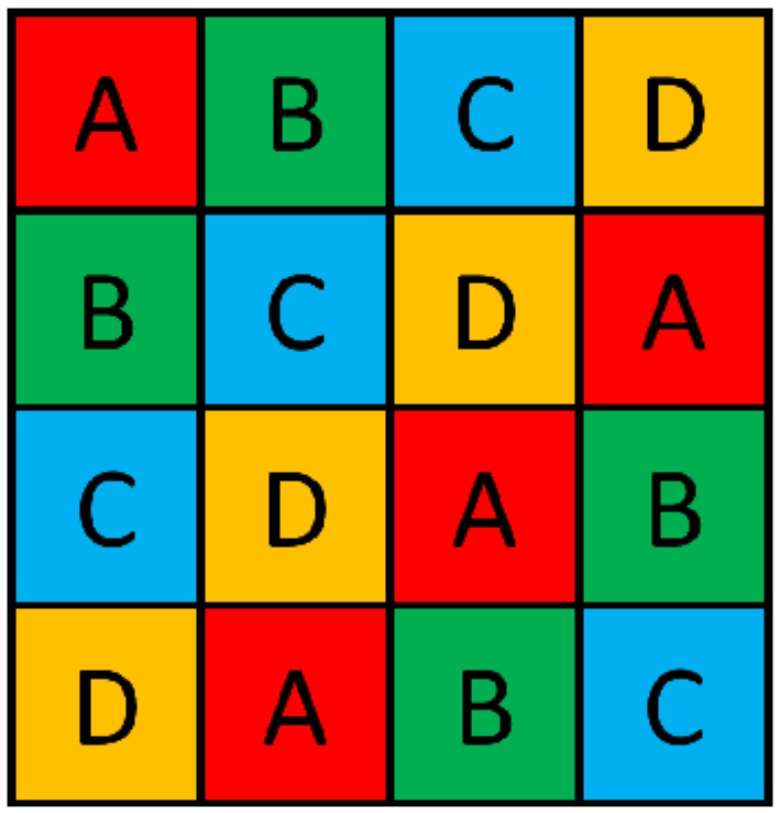
پس از اختصاص تصادفی بلوکها به ردیفها و ستونها، مربع لاتین ما به شکل زیر در میآید. حروف تیمار معادل انواع خاص کود هستند.
| خاک غنی | متوسط غنی | خاک متوسط | خاک فقیر | |
| نور خورشید متوسط-کم | A | B | C | D |
| نور خورشید کم | B | C | D | A |
| نور خورشید متوسط-زیاد | C | D | A | B |
| نور خورشید زیاد | D | A | B | C |
هر سلول یک واحد آزمایشی منحصر به فرد است که یک تیمار خاص را در ترکیبی خاص از شرایط انسداد سطر و ستون دریافت میکند.
مرحله 3: انجام آزمایش
برای انجام آزمایش، یک گیاه را در هر سلول شبکه قرار دهید. هر گیاه تیمار اختصاص داده شده به آن سلول را دریافت میکند. آزمایشگران باید ترتیب اندازهگیری، آبیاری یا تعامل با هر گیاه را به صورت تصادفی تنظیم کنند تا از ایجاد سوگیری در طول زمان جلوگیری شود. برای 16 واحد آزمایشی یک ترتیب اجرای تصادفی ایجاد کنید و مطالعه را با پیروی از آن ترتیب انجام دهید.
نحوه تجزیه و تحلیل یک مربع لاتین
پس از اتمام آزمایش، میتوانید نتایج را با استفاده از آنالیز واریانس مدل خطی عمومی (GLM) تجزیه و تحلیل کنید. این روش آماری انعطافپذیر به شما امکان میدهد چندین عامل دستهبندی را در مدل بگنجانید – مانند تیمار، سطر (فاکتور انسداد 1) و ستون (فاکتور انسداد 2).
- تیمار
- ردیف (فاکتور انسداد 1)
- ستون (فاکتور انسداد 2)
این رویکرد به شما امکان میدهد تا ضمن کنترل تغییرپذیری ناشی از عوامل انسداد سطر و ستون، اثر تیمار را آزمایش کنید. فقط به یاد داشته باشید، این تحلیل فرض میکند که هیچ تعاملی بین متغیرهای تیمار و مزاحم وجود ندارد، که یکی از فرضیات کلیدی طرح مربع لاتین است. عبارات تعاملی را نمیتوان در این طرح تخمین زد زیرا هر ترکیب تیمار-سطر-ستون فقط یک بار ظاهر میشود و هیچ تکرار برای جدا کردن اثرات تعاملی از خطا باقی نمیگذارد.
علاوه بر فرض عدم تعامل، تحلیل مربع لاتین بر فرضیات استاندارد مدل خطی عمومی متکی است. این فرضیات شامل استقلال مشاهدات، نرمال بودن باقیماندهها و همگنی واریانس در سطوح تیمار و بلوک است. نقض این فرضیات میتواند بر قابلیت اطمینان نتایج تأثیر بگذارد.
مربعهای لاتین ممکن است انعطافپذیرترین طرح نباشند، اما وقتی به درستی استفاده شوند، یک راهحل زیبا برای کنترل دو عامل مزاحم با حداقل واحدهای آزمایشی ارائه میدهند.





پاسخگوی سوالات و نظرات شما هستیم