
ضریب تغییرات در آمار
ضریب تغییرات چیست؟
ضریب تغییرات (CV) (Coefficient of variation) یک معیار نسبی از تغییرپذیری است که اندازه انحراف معیار را نسبت به میانگین آن نشان میدهد. این یک معیار استاندارد و بدون واحد است که به شما امکان میدهد تغییرپذیری را بین گروهها و ویژگیهای متفاوت مقایسه کنید. همچنین به عنوان انحراف معیار نسبی (RSD) شناخته میشود.
در این پست، در مورد ضریب تغییرات، نحوه محاسبه آن، دانستن اینکه چه زمانی به طور خاص مفید است و چه زمانی باید از آن اجتناب کرد، خواهید آموخت.
نحوه محاسبه ضریب تغییرات
محاسبه ضریب تغییرات شامل یک نسبت ساده است. به سادگی انحراف معیار را بگیرید و آن را بر میانگین تقسیم کنید.
فرمول ضریب تغییرات: انحراف معیار/میانگین (انحراف معیار تقسیم بر میانگین)
مقادیر بالاتر نشان میدهد که انحراف معیار در مقایسه با میانگین نسبتاً بزرگ است.
به عنوان مثال، یک رستوران پیتزا زمان تحویل خود را بر حسب دقیقه اندازهگیری میکند. میانگین زمان تحویل ۲۰ دقیقه و انحراف معیار ۵ دقیقه است. پس ضریب تغییرات 0.25 خواهد بود.
تفسیر ضریب تغییرات
برای مثال تحویل پیتزا، ضریب تغییرات 0.25 است. این مقدار، اندازه نسبی انحراف معیار را در مقایسه با میانگین به شما نشان میدهد. تحلیلگران اغلب ضریب تغییرات را به صورت درصد گزارش میکنند. در این مثال، انحراف معیار 25٪ اندازه میانگین است.
اگر مقدار برابر با یک یا 100٪ باشد، انحراف معیار برابر با میانگین است. مقادیر کمتر از یک نشان میدهد که انحراف معیار کوچکتر از میانگین (معمولاً) است، در حالی که مقادیر بزرگتر از یک زمانی رخ میدهند که انحراف معیار بزرگتر از میانگین باشد.
به طور کلی، مقادیر بالاتر نشان دهنده درجه بیشتری از تغییرپذیری نسبی هستند.
معیارهای مطلق در مقابل معیارهای نسبی تغییرپذیری
نموداری که توزیعهای نرمال را با انحراف معیارهای مختلف نشان میدهد. در پست دیگری، در مورد انحراف معیار، دامنه بین چارکی و دامنه صحبت خواهیم کرد. این آمارهها، معیارهای مطلق تغییرپذیری هستند. این موارد از واحد اندازهگیری متغیر برای توصیف تغییرپذیری استفاده میکنند.
برای انحراف معیار پنج دقیقهای در مثال تحویل پیتزا، میدانیم که تحویل معمول پنج دقیقه قبل یا بعد از میانگین زمان تحویل رخ میدهد.
این اطلاعات بسیار مفید است! این نمودار، تغییرپذیری دادههای ما را با استفاده از واحدهای اندازهگیری اصلی، به راحتی، نشان میدهد. میتوانیم این تغییرپذیری زمان تحویل را با یک رستوران پیتزای دیگر مقایسه کنیم.
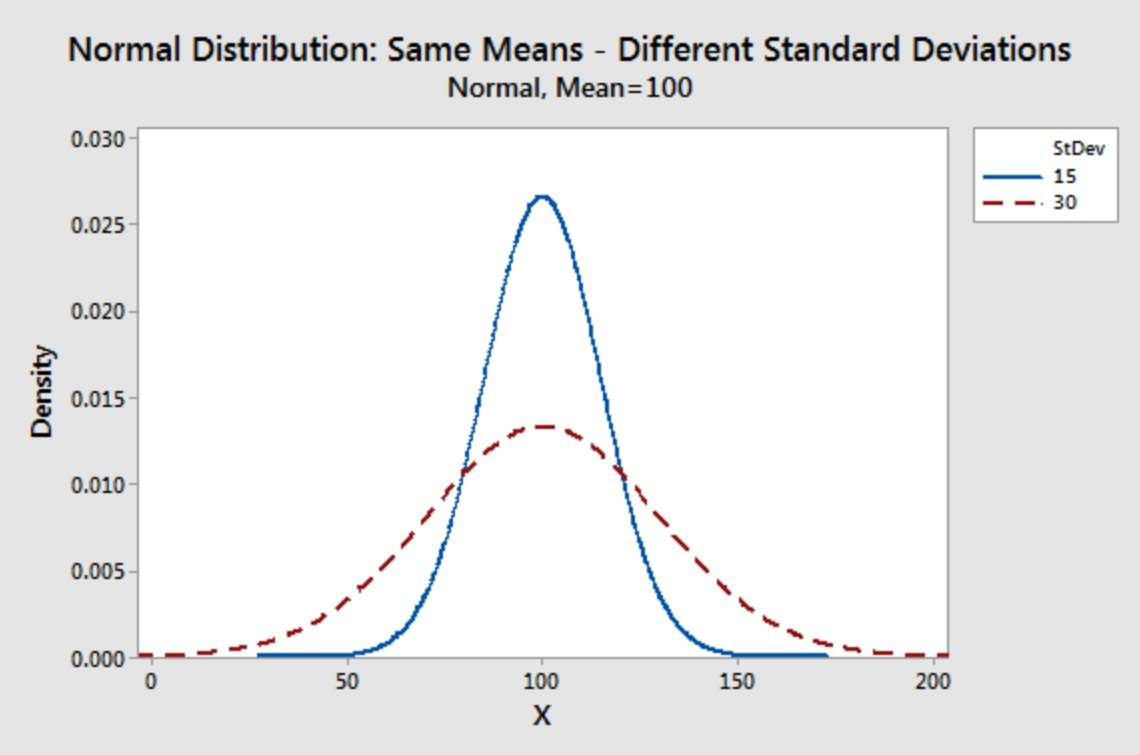
از سوی دیگر، اندازهگیریهای نسبی از یک فرآیند استانداردسازی استفاده میکنند که واحدهای اندازهگیری اصلی را حذف میکند. در نسبت CV، هم انحراف معیار و هم میانگین از واحدهای یکسانی استفاده میکنند که آنها را خنثی میکند و یک آماره بدون واحد تولید میکند.
چه زمانی میخواهید از ضریب تغییرات استفاده کنید؟ ماهیت بدون واحد آن مزایایی را برای آن فراهم میکند. به طور خاص، ضریب تغییرات مقایسههای معناداری را در سناریوهایی که معیارهای مطلق نمیتوانند مقایسه کنند، تسهیل میکند.
وقتی میخواهید تغییرپذیری را بین موارد زیر مقایسه کنید، از ضریب تغییرات استفاده کنید:
- گروههایی که میانگینهایی با بزرگی بسیار متفاوت دارند.
- ویژگیهایی که از واحدهای اندازهگیری متفاوتی استفاده میکنند.
در این دو مورد، معیارهای مطلق میتوانند مشکلساز باشند. بیایید بیشتر بررسی کنیم!
استفاده از ضریب تغییرات وقتی میانگینها بسیار متفاوت هستند:
وقتی ویژگیای را اندازهگیری میکنید که طیف وسیعی از مقادیر را دارد، اغلب انتظار دارید که میانگین و انحراف معیار با هم تغییر کنند. این پدیده اغلب در دادههای مقطعی رخ میدهد. در این موارد، میخواهید بدانید که انحراف معیار نسبت به میانگینهای بسیار متفاوت چگونه است.
فرض کنید در حال اندازهگیری هزینههای خانوار هستید و میخواهید تغییرپذیری هزینهها را بین خانوارهای پردرآمد و کمدرآمد مقایسه کنید. این دادهها فرضی هستند.
| هزینه ها | درآمد بالا | درآمد پایین |
| میانگین | 500000 دلار | 40000 دلار |
| انحراف معیار | 125000 دلار | 10 هزار دلار |
این مقادیر از واحد اندازهگیری یکسانی (دلار آمریکا) استفاده میکنند و به شما امکان میدهند انحرافات معیار را مقایسه کنید. تغییرپذیری در هزینههای خانوارهای پردرآمد بسیار بیشتر از خانوارهای کمدرآمد است (۱۲۵۰۰۰ دلار انحراف معیار در مقابل ۱۰۰۰۰ دلار انحراف معیار). با این حال، با توجه به تفاوت زیاد در میانگین هزینهها، این تعجبآور نیست.
با این حال، اگر میخواهید تغییرپذیری را با در نظر گرفتن میانگینهای متفاوت مقایسه کنید، باید از یک معیار نسبی تغییرپذیری، مانند ضریب تغییرات، استفاده کنید. جدول زیر نشان میدهد که وقتی تفاوت در هزینهها را در نظر میگیرید، گروه کمدرآمد در واقع تغییرپذیری برابری دارد.
| ضریب تغییرات | درآمد بالا | درآمد پایین |
| 25% | 25% |
مثالهای دنیای واقعی
تحلیلگران اغلب زمانی از ضریب تغییرپذیری استفاده میکنند که مجموعه دادههایشان طیف وسیعی از میانگینها را داشته باشد، همانطور که در مثال قبلی نشان داده شده است.
محققان از CV برای ارزیابی نابرابری درآمدها در کشورهای مختلف استفاده میکنند. میانگین درآمدها بر اساس کشور بسیار متفاوت است. کشورهای ثروتمند و کشورهای فقیر وجود دارند. برای در نظر گرفتن نابرابری در هر کشور ضمن در نظر گرفتن میانگین درآمدهای بسیار متفاوت، تحلیلگران از ضریب تغییرپذیری استفاده میکنند. در این زمینه، وقتی کشوری ضریب تغییرپذیری بیشتری دارد، نشاندهنده درجه بیشتری از نابرابری درآمدی است.
به طور مشابه، تحلیلگران مالی از ضریب تغییرپذیری برای ارزیابی نوسانات بازده سرمایهگذاریهای مالی در طیف وسیعی از ارزشگذاریها استفاده میکنند. در این زمینه، ضرایب بالاتر نشاندهنده ریسک قابل توجهتری هستند.
ضریب تغییرپذیری به ویژه زمانی مفید است که دادههای شما از توزیع لگاریتمی نرمال پیروی میکنند. در این توزیعها، انحراف معیار بسته به بخشی از توزیع که ارزیابی میکنید تغییر میکند. با این حال، ضریب تغییر در سراسر توزیع لگاریتمی نرمال ثابت میماند.
استفاده از ضریب تغییرات برای مقایسه اندازهگیریهایی که از واحدهای مختلف استفاده میکنند
وقتی اندازهگیریها از مقیاسهای مختلف استفاده میکنند، نمیتوانید آنها را مستقیماً مقایسه کنید. فرض کنید میخواهید تغییرپذیری نمرات SAT را با نمرات ACT مقایسه کنید؟ اگرچه این آزمونهای ورودی دانشگاه از نظر ماهیت و هدف مشابه هستند، اما از مقیاسهای متفاوتی استفاده میکنند. در نتیجه، نمیتوانید انحراف معیار آنها را مستقیماً مقایسه کنید.
با این حال، ضریب تغییرات دادههای خام را استاندارد میکند، به این معنی که میتوانید تغییرپذیری نسبی نمرات SAT و ACT را مقایسه کنید.
علاوه بر این، هر زمان که میخواهید تغییرپذیری ویژگیهای ذاتاً متفاوت را ارزیابی کنید، باید از یک معیار نسبی تغییرپذیری، مانند ضریب تغییرپذیری، استفاده کنید. به عنوان مثال، ممکن است بخواهید تغییرپذیری دمای عملیاتی و سرعت هواپیماها را ارزیابی کنید. یا تغییرپذیری وزن و مقاومت نمونههای مواد را مقایسه کنید. نمیتوانید انحراف معیارها را که از واحدهای مختلف استفاده میکنند، مانند کیلوگرم برای وزن و مگاپاسکال برای استحکام، به طور معناداری مقایسه کنید!
با این حال، اگر متغیر کیلوگرم شما ضریب تغییرپذیری بالاتری نسبت به مگاپاسکال داشته باشد، میدانید که وزن نسبتاً متغیرتر از استحکام است.
این مثالها ویژگیهای کاملاً متفاوتی را با استفاده از واحدهای مختلف اندازهگیری میکنند. با این حال، میتوانید از ضریب تغییرات برای مقایسه تغییرپذیری نسبی آنها استفاده کنید!
هشدارهایی در مورد زمان عدم استفاده از ضریب تغییرات
در حالی که ضریب تغییرات در برخی زمینهها بسیار مفید است، مواردی وجود دارد که نباید از آن استفاده کنید.
وقتی میانگین نزدیک به صفر است از آن استفاده نکنید.
اگر میانگین برابر با صفر باشد، مخرج نسبت صفر است که مشکلساز است! خوشبختانه، بعید است میانگینی داشته باشید که دقیقاً برابر با صفر باشد. اما وقتی میانگین نزدیک به صفر باشد، ضریب تغییرات میتواند به بینهایت نزدیک شود و مقدار آن مستعد تغییرات کوچک در میانگین است!
با مقیاسهای فاصلهای استفاده نکنید.
از ضریب تغییرات فقط زمانی استفاده کنید که دادههای شما از مقیاس نسبتی استفاده میکنند. از آن برای مقیاسهای فاصلهای استفاده نکنید.
مقیاسهای نسبتی دارای صفر مطلق هستند که نشان دهنده فقدان کامل ویژگی است. به عنوان مثال، وزن صفر (با استفاده از سیستم امپریال یا متریک) نشان دهنده فقدان کامل وزن است. وزن یک مقیاس نسبتی است.
با این حال، دماها بر اساس فارنهایت و سلسیوس مقیاسهای فاصلهای هستند. این سیستمهای اندازهگیری دارای مقدار صفر هستند، اما این صفرها نشاندهندهی عدم وجود دما نیستند. (کلوین دارای صفر مطلق است که نشاندهندهی عدم وجود دما است. کلوین یک مقیاس نسبی است.)
مقیاسهای فاصلهای به شما اجازه نمیدهند اندازهگیریها را به شیوهای معنادار تقسیم کنید. به عنوان مثال، 10 درجه سانتیگراد 1/3 دمای 30 درجه سانتیگراد نیست! از آنجا که ضریب تغییرات شامل تقسیم است، این آماره برای مقیاسهای فاصلهای بیمعنی است.
بیایید مثالی از مشکلی که هنگام استفاده از ضریب تغییرات با مقیاسهای فاصلهای رخ میدهد را ببینیم!
جدول زیر جفت دماهای معادل را نشان میدهد. انتظار میرود ضرایب تغییرات آنها برابر باشد. بیایید بررسی کنیم!
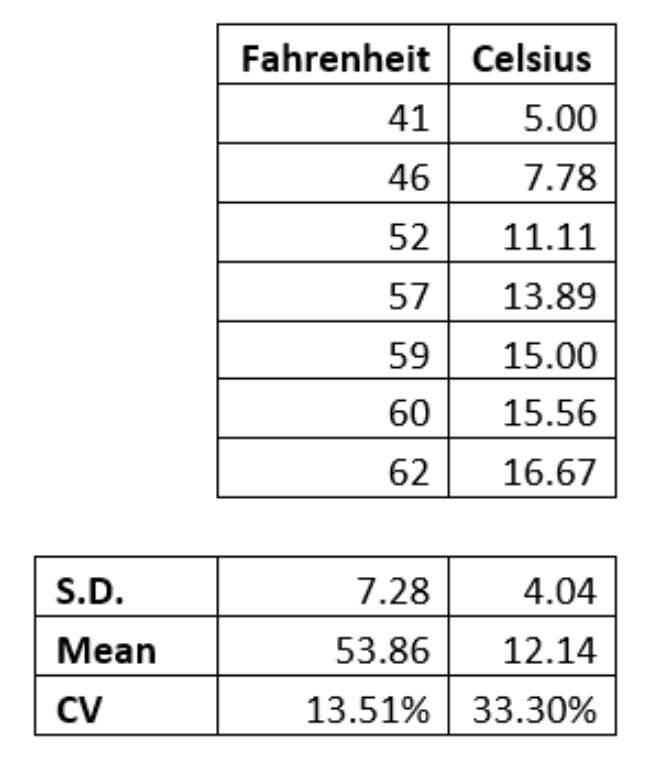
ضرایب تغییرات کاملاً متفاوت هستند! این به این دلیل است که ما در حال ارزیابی مقیاسهای فاصلهای هستیم.
از ضریب تغییرات فقط زمانی استفاده کنید که در مقیاس نسبتی، صفر مطلق واقعی داشته باشید!
معیارهای مطلق در مقابل نسبی در سایر زمینههای آماری
نیاز به انتخاب بین استفاده از یک معیار مطلق (مثلاً انحراف معیار) در مقابل یک معیار نسبی و استاندارد شده (مثلاً ضریب تغییرات) در جای دیگری از آمار نیز وجود دارد.



پاسخگوی سوالات و نظرات شما هستیم