همبستگی کاذب: توضیح کامل با مثال
همبستگی کاذب چیست؟
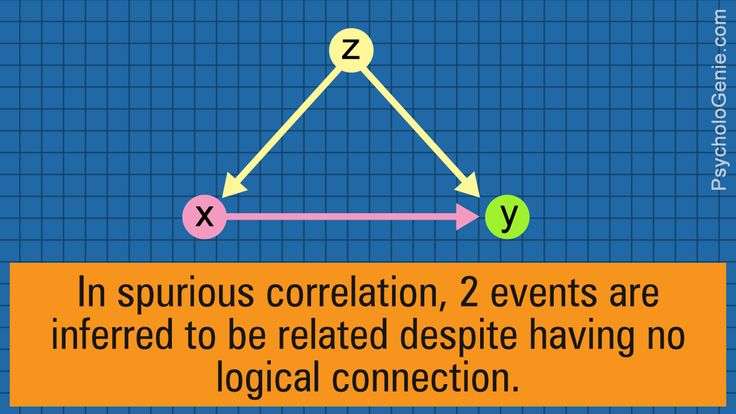
همبستگی کاذب یا جعلی (Spurious correlation) زمانی رخ میدهد که دو متغیر با هم همبستگی دارند اما رابطه علّی ندارند. به عبارت دیگر، به نظر میرسد که مقادیر یک متغیر باعث تغییر در متغیر دیگر میشود، اما در واقع این اتفاق نمیافتد.
اگر تعریف کاذب را جستجو کنید، توضیحاتی در مورد جعلی بودن یا ماهیت فریبنده چیزی خواهید دید. ظاهر بیرونی آن اصالت دارد، اما تقلیدی است. با در نظر گرفتن این تعریف، همبستگیهای کاذب هم در معیارهای آماری و هم در نمودارها مانند روابط علّی به نظر میرسند، اما واقعی نیستند.
به عنوان مثال، فروش بستنی و حمله کوسه در ساحل همبستگی مثبتی دارند. با افزایش فروش بستنی، حملات کوسه بیشتر میشود. با این حال، عقل سلیم به ما میگوید که فروش بستنی باعث حمله کوسه نمیشود. از این رو، این یک همبستگی کاذب است.
همبستگیهای کاذب میتوانند به شکل ضرایب همبستگی غیر صفر و به عنوان الگوهایی در یک نمودار ظاهر شوند. برای مثال، در مثال زیر از tylervigen.com، همبستگی بین واردات نفت خام ایالات متحده از نروژ و رانندگانی که در اثر برخورد با قطار کشته شدهاند، ضریب همبستگی بسیار بالایی برابر با +0.95 دارد که نشان دهنده یک رابطه قوی و مثبت است. نمودار این دادهها، همانطور که در زیر نشان داده شده است، این همبستگی را تأیید میکند.
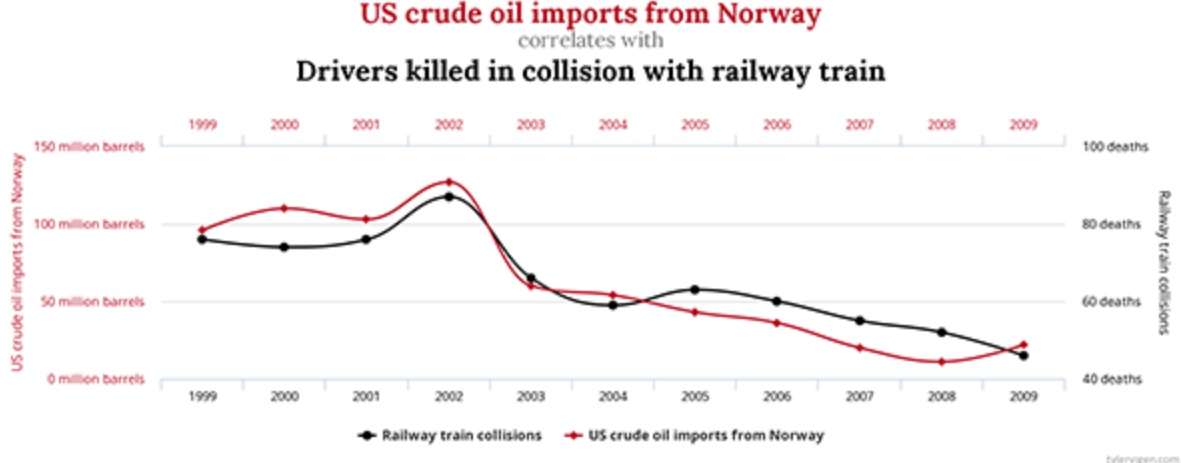
صد البته، هیچ رابطهی علّی بین این دو وجود ندارد!
محققان باید روابط علّی واقعی را شناسایی کنند، که شامل رد احتمال همبستگیهای کاذب است.
در این پست، یاد خواهید گرفت که چگونه همبستگیهای کاذب رخ میدهند، چگونه آنها را شناسایی کنید و روشهای جلوگیری از آنها را بیاموزید.
چه چیزی باعث همبستگی کاذب میشود؟
همبستگیهای کاذب به دلایل مختلفی رخ میدهند. تمام توضیحات زیر میتوانند یک همبستگی کاذب ایجاد کنند که ضریب همبستگی غیر صفر و نموداری را نشان میدهد که یک رابطه را نشان میدهد.
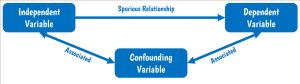
متغیرهای مخدوشکننده
مخدوشگری زمانی رخ میدهد که یک متغیر سوم باعث ایجاد تغییر در دو متغیر دیگر میشود و یک همبستگی کاذب بین دو متغیر دیگر ایجاد میکند. به عنوان مثال، تصور کنید که دو رابطه علّی مثبت زیر وجود دارند.
- A → B
- A → C
با افزایش A، B و C هر دو با هم افزایش مییابند. از این رو، به نظر میرسد که B → C.
به عنوان مثال، دمای بالاتر باعث میشود افراد بیشتری بستنی بخرند و در ساحل شنا کنند و فرصتهای حمله کوسه را افزایش دهند. از این رو، اگرچه هیچ رابطهای بین فروش بستنی و حمله کوسه وجود ندارد، اما آنها تمایل دارند با هم افزایش و کاهش یابند. متغیر مخدوشکننده دما باعث این همبستگی کاذب میشود.
متغیرهای میانجی
در موارد دیگر، زنجیرهای از همبستگیها یا متغیرهای میانجی، یک همبستگی کاذب ایجاد میکنند. برای مثال، تصور کنید که هم A و B و هم B و C روابط علّی دارند، همانطور که در زیر نشان داده شده است.
A → B → C.
اگر فقط اندازهگیریهای A و C را داشته باشید، یک همبستگی کاذب پیدا خواهید کرد. به نظر میرسد که این همبستگی علّی است. در واقعیت، A باعث B میشود و سپس B باعث C میشود. هیچ ارتباط مستقیمی بین A و C وجود ندارد.
خطای نمونهگیری تصادفی
نمونهها به دلیل شانس، همیشه به طور دقیق منعکسکننده جمعیت نیستند. خطای نمونهگیری تصادفی میتواند باعث بروز اثراتی در نمونه شود که در جمعیت وجود ندارند. همبستگی یکی از اثرات احتمالی است.
برای مطالعاتی که از نمونهها استفاده میکنند، همبستگیهایی که پیدا میکنید ممکن است در جمعیت وجود نداشته باشند. آزمون فرضیه میتواند به حل این مشکل کمک کند.
وقتی همبستگیها در یک نمونه در جمعیت وجود ندارند، این یک شبح است که خطای تصادفی ایجاد کرده است و از این رو، نمیتواند یک رابطه علی باشد. در نتیجه، این یک همبستگی کاذب است. نمونهها کامل نیستند.
شانس
در برخی موارد، صرفاً شانس محض است که دو متغیر متفاوت از الگوی مشابهی پیروی کنند که شبیه یک رابطه است. این وضعیت کمی با خطای نمونهگیری تصادفی متفاوت است. در این حالت، مقادیر دو متغیر در جمعیت با هم همبستگی دارند. این یک سراب ناشی از یک نمونه نیست. با این حال، هیچ رابطه علی بین دو متغیر وجود ندارد. الگوهای تغییرات به طور تصادفی با هم مطابقت دارند.
دستکاری گرافیکی
با تنظیم مقیاسهای نمودار، الگوهای تغییرات در دو متغیر را میتوان اغراقآمیز یا کوچک کرد تا دو الگو با هم مطابقت داشته باشند. اما این فقط نتیجه دستکاری دقیق مقیاس است. این فرآیند یک همبستگی کاذب ایجاد میکند.
تشخیص و جلوگیری از همبستگیهای کاذب
بهترین راه برای تشخیص همبستگی کاذب از طریق دانش موضوعی است. ایجاد روابط علی میتواند دشوار باشد. هیچ آزمون آماری وجود ندارد که بتواند آن را اثبات کند. در عوض، تحلیلگران اغلب باید علل و جعلی بودن سایر موارد را رد کنند. درباره همبستگی در مقابل علیت: درک تفاوتها بیشتر بدانید.
از دانش موضوعی خود برای ارزیابی همبستگیها استفاده کنید و سوالات زیادی بپرسید:
- آیا آنها به عنوان روابط علّی منطقی هستند؟
- آیا با نظریههای اثباتشده مطابقت دارند؟
- آیا میتوانید مکانیسمی برای علیت پیدا کنید؟
- آیا ارتباط مستقیمی وجود دارد یا متغیرهای واسطهای دخیل هستند؟
معیارهای زیادی میتوانند به شما در ارزیابی همبستگیها کمک کنند. برای اطلاعات بیشتر، پستی را راجع به معیارهای هیل برای علیت در قالب چند مثال بررسی خواهیم کرد.
روشهای آماری و تجربی مختلف میتوانند به کاهش همبستگیهای کاذب کمک کنند. به طور خاص، این روشها میتوانند از ایجاد همبستگیهای کاذب توسط متغیرهای مخدوشکننده جلوگیری کنند.
در یک مطالعه تصادفی، تصادفیسازی معمولا عوامل مخدوشکننده را بین گروههای آزمایشی برابر می کند و در نتیجه، خطر همبستگی کاذب را کاهش دهد. علاوه بر این، میتوانید از متغیرهای کنترل برای حفظ شرایط آزمایش تا حد امکان استفاده کنید. درباره انتساب تصادفی در آزمایشها بیشتر بدانید.
همسانسازی تکنیک دیگری است که میتواند خطر همبستگیهای کاذب ناشی از عوامل مخدوشکننده را کاهش دهد. این فرآیند شامل انتخاب شرکتکنندگان در مطالعه با ویژگیهای مشابه خارج از متغیر مورد نظر برای گروههای درمان و کنترل است.
تحلیل رگرسیون چندگانه میتواند با استفاده از مدلهایی که متغیرهای مخدوشکننده را در نظر میگیرند، از همبستگی کاذب جلوگیری کند. این رویکرد از نظر آماری عوامل مخدوشکننده را کنترل میکند.
برعکس، مطالعات همبستگی در تحقیقات اولیه به سرعت و به راحتی روابط را پیدا میکنند، اما برای ایجاد علیت مناسب نیستند.




پاسخگوی سوالات و نظرات شما هستیم