کشیدگی (Kurtosis) و چولگی (Skewness) در آمار
کشیدگی (Kurtosis)
کشیدگی یک معیار آماری است که برای توصیف میزان تجمع نمرات در دنبالهها یا قله توزیع فراوانی استفاده میشود. در واقع کشیدگی غیرمزوکورتیک با حالت منحنی نرمال یا زنگوله ای در تضاد است. اگر توزیع ما نرمال باشد، دیگر کشیدگی لپتوکورتیک و یا پلاتیکورتیک نداریم.
قله بلندترین قسمت توزیع است و دنبالهها انتهای توزیع هستند.
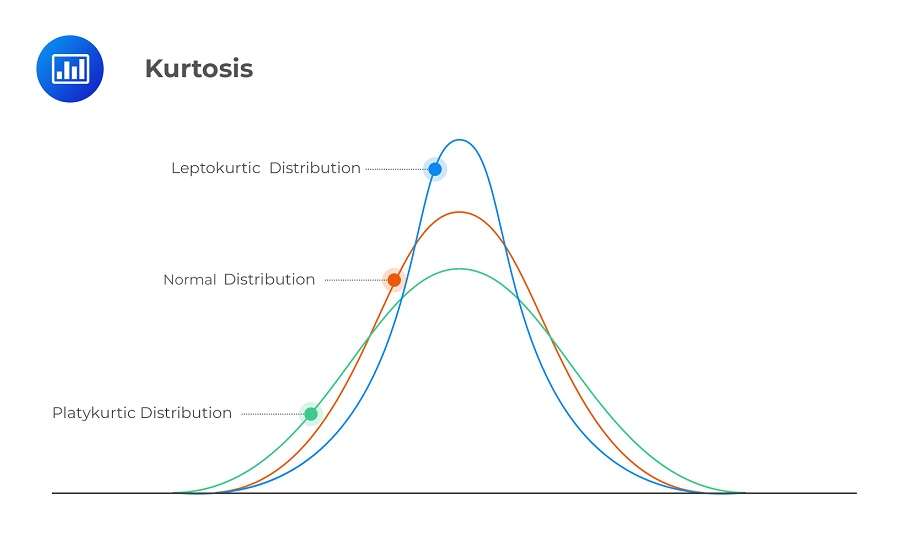
سه نوع کشیدگی وجود دارد: مزوکورت، لپتوکورتیک و پلاتیکورتیک.

- کشیدگی مزوکورت: توزیعهایی که از نظر پهنا و منحنیها متوسط هستند و ارتفاع اوج متوسطی دارند.
- کشیدگی لپتوکورتیک: مقادیر بیشتری در دنبالههای توزیع و مقادیر بیشتری نزدیک به میانگین (یعنی با قلههای تیز و دنبالههای ضخیم)
- کشیدگی پهن یا پهن کش (پلاتیکورتیک): مقادیر کمتری در دنبالهها و مقادیر کمتری نزدیک به میانگین (یعنی منحنی دارای قلهای مسطح است و نمرات پراکندهتر با دنبالههای روشنتر دارد).
کشیدگی نرمال
وقتی کشیدگی برابر با ۳ باشد، توزیع مزوکورت است.
این بدان معناست که کشیدگی مشابه توزیع نرمال است؛ مزوکورت (اوج متوسط) است.
کشیدگی یک توزیع مزوکورت نه زیاد است و نه کم؛ بلکه به عنوان مبنایی برای دو طبقهبندی دیگر در نظر گرفته میشود.
وقتی کشیدگی صفر باشد
وقتی کشیدگی برابر با ۰ باشد، توزیع پهنکش است.
توزیع پهنکش در مقایسه با توزیع نرمال، مسطحتر (با پیک کمتر) است و مقادیر کمتری در دنبالههای کوتاهتر (یعنی روشنتر و نازکتر) خود دارد.

کشیدگی منفی
مقادیر اضافی منفی کشیدگی (<3) نشان میدهد که توزیع مسطح است و دنبالههای نازکی دارد. توزیعهای کشیدگی پلاتیکورتیک مقادیر کشیدگی منفی دارند.
توزیع کشیدگی پلاتیکورتیک در مقایسه با توزیع نرمال، مسطحتر (با پیک کمتر) است و مقادیر کمتری در دنبالههای کوتاهتر (یعنی روشنتر و نازکتر) خود دارد.

کشیدگی مثبت
مقادیر مثبت اضافی کشیدگی (> 3) نشان میدهد که توزیع دارای قله و دنبالههای ضخیم است. توزیعهای لپتوکورتیک دارای مقادیر کشیدگی مثبت هستند.
یک توزیع لپتوکورتیک در مقایسه با توزیع نرمال، قله بلندتر (زنگ نازک) و دنبالههای بلندتر (یعنی ضخیمتر و سنگینتر) دارد.

یک کشیدگی مثبت شدید، توزیعی را نشان میدهد که در آن بیشتر مقادیر در دنبالههای توزیع قرار دارند تا در اطراف میانگین.
چولگی (skewness)
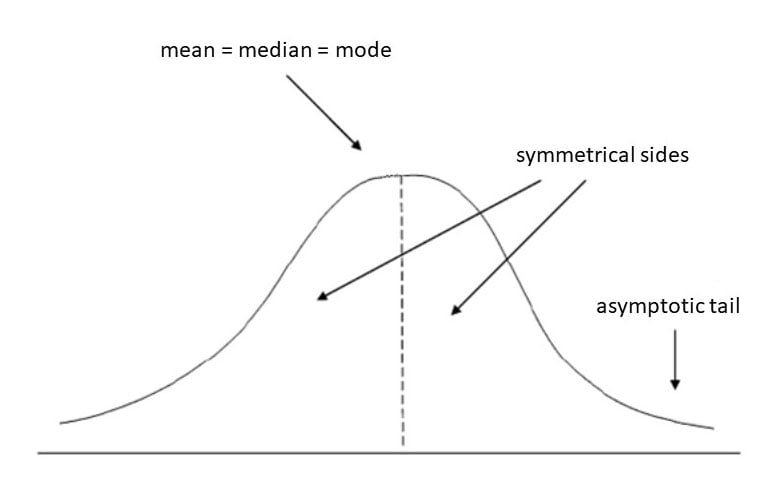
چولگی یک معیار آماری است که عدم تقارن یک توزیع را توصیف میکند. این معیار نشان میدهد که آیا مقادیر دادهها بیشتر در سمت چپ یا راست مرکز پخش شدهاند. یک توزیع کاملاً متقارن، مانند توزیع نرمال، چولگی صفر دارد.
چولگی به شما کمک میکند تا شکل دادههای خود و اینکه آیا بخش عمدهای از مقادیر در یک طرف میانگین قرار دارند یا خیر را درک کنید. این امر به ویژه هنگام ارزیابی اینکه آیا دادهها فرض نرمال بودن را در تحلیلهای آماری برآورده میکنند یا خیر، مفید است.
انواع چولگی
شما معمولاً میتوانید با ارزیابی بصری یک نمودار، وجود و نوع چولگی را در یک توزیع تشخیص دهید.
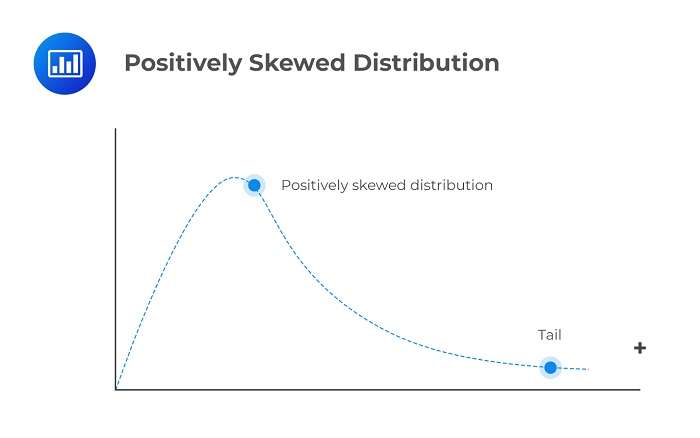
راست یا مثبت
دم در سمت راست قله بلندتر است. میانگین بزرگتر از میانه است.
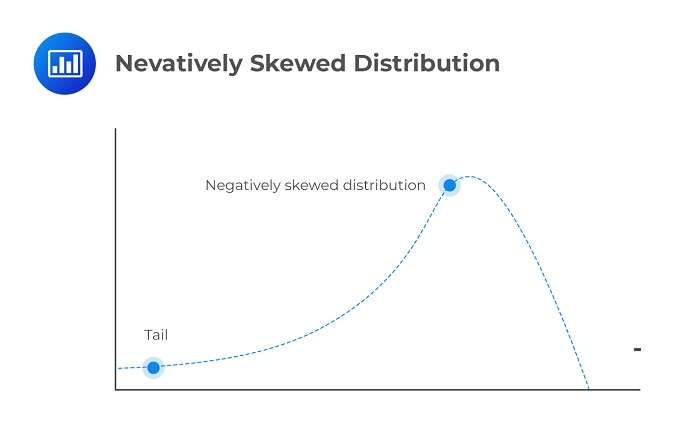
چپ یا منفی
دم سمت چپ بلندتر است. میانگین از میانه کوچکتر است.
صفر
توزیع متقارن است. میانگین و میانه تقریباً برابرند.
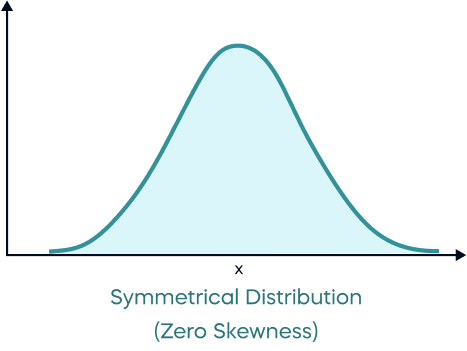
نحوه محاسبه چولگی
فرمولهای متعددی برای اندازهگیری چولگی وجود دارد. یکی از سادهترین و شهودیترین آنها، چولگی میانه پیرسون است. این فرمول از این واقعیت بهره میبرد که میانگین و میانه در یک توزیع چولگی متفاوت هستند.

این فرمول به شما میگوید که چند انحراف معیار، میانگین و میانه را از هم جدا میکند. مقدار مثبت نشاندهندهی چولگی به راست و مقدار منفی نشاندهندهی چولگی به چپ است.
مجموعه دادههای دنیای واقعی به ندرت دارای مقدار چولگی میانه پیرسون دقیقاً صفر هستند. اگر دادههای شما مقداری نزدیک به ۰ داشته باشند، میتوانید آن را متقارن در نظر بگیرید. هیچ حد آستانهی جهانی برای «به اندازهی کافی نزدیک» وجود ندارد، اما برخی از محققان پیشنهاد میکنند که مقادیر بین -۰.۴ و ۰.۴ نشاندهندهی توزیع تقریباً متقارن در نمونههای بزرگ هستند.
مثال چولگی
مجموعهای از درآمد خانوارها نشان میدهد که اکثر خانوارها بین ۳۰،۰۰۰ تا ۷۰،۰۰۰ دلار درآمد دارند، اما تعداد کمی از آنها بیش از ۱ میلیون دلار درآمد دارند. توزیع دارای یک دنباله بلند به راست است که آن را چولگی مثبت میکند. در این حالت، میانگین درآمد به دلیل چند مقدار افراطی بالاتر از میانه قرار میگیرد.

درک چولگی به تحلیلگران کمک میکند تا آمارههای خلاصه مناسب را انتخاب کنند و تعیین کنند که آیا برای تحلیل بیشتر به تبدیلها یا روشهای ناپارامتری نیاز است یا خیر.




پاسخگوی سوالات و نظرات شما هستیم