آزمون تی تک نمونه‌ای: تعریف، کاربرد و مثال

آزمون تی تک نمونه‌ای چیست؟

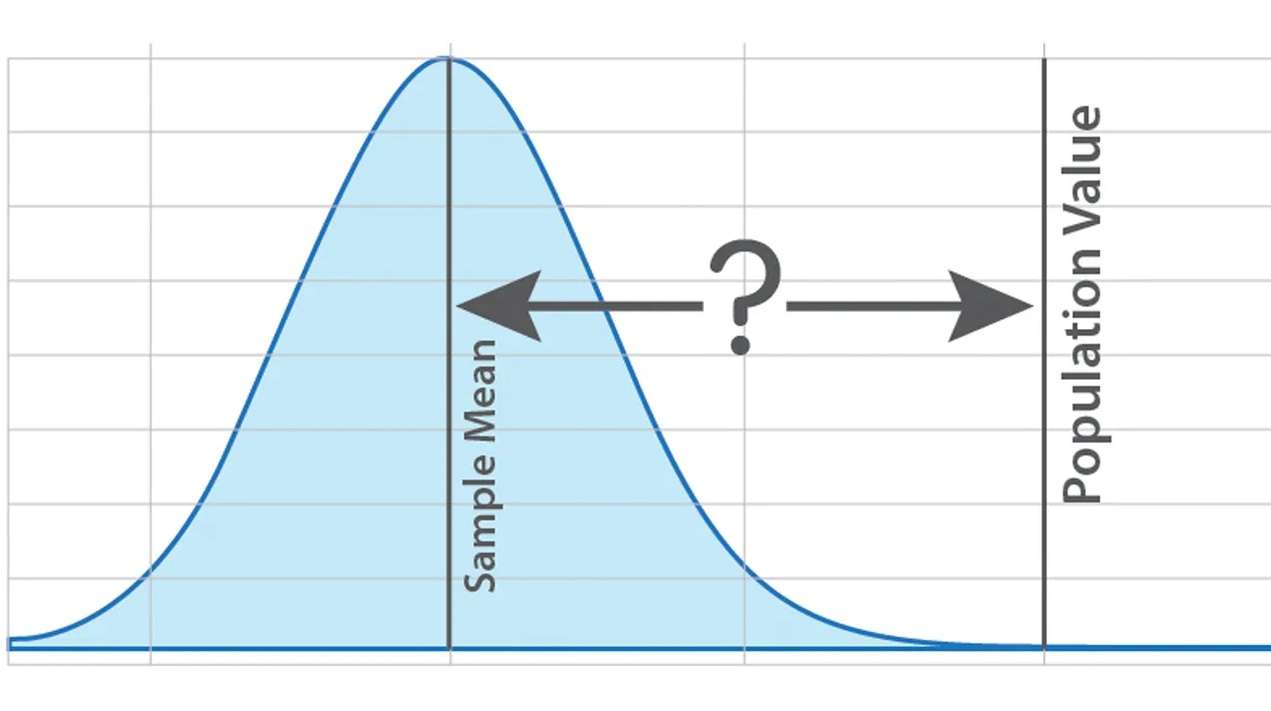
از آزمون تی تک نمونه‌ای برای ارزیابی میانگین جمعیت با استفاده از یک نمونه واحد استفاده کنید. شما معمولاً این آزمون فرضیه را برای تعیین اینکه آیا میانگین جمعیت با مقدار فرضی که شما مشخص می‌کنید متفاوت است یا خیر، انجام می‌دهید. مقدار فرضی می‌تواند از نظر تئوری در حوزه مورد مطالعه، یک مقدار مرجع یا یک هدف مهم باشد.

به عنوان مثال، یک شرکت نوشیدنی ادعا می‌کند که قوطی‌های نوشابه آن حاوی ۱۲ اونس است. یک محقق به طور تصادفی از قوطی‌های آنها نمونه‌برداری می‌کند و مقدار مایع موجود در هر یک را اندازه‌گیری می‌کند. آزمون تی تک نمونه‌ای می‌تواند از داده‌های نمونه برای تعیین اینکه آیا کل جمعیت قوطی‌های نوشابه با مقدار فرضی ۱۲ اونس متفاوت است یا خیر، استفاده کند.

در این پست، در مورد آزمون تی تک نمونه‌ای، فرضیه‌ها و فرضیات آن و نحوه تفسیر نتایج یاد می گیریم.

فرضیه‌های آزمون T تک نمونه‌ای

آزمون T تک نمونه‌ای فرضیه‌های زیر را دارد:

• فرضیه صفر (H0): میانگین جمعیت برابر با مقدار فرضی است (µ = H0).
• فرضیه جایگزین (HA): میانگین جمعیت برابر با مقدار فرضی نیست (µ ≠ H0).

اگر مقدار p کمتر از سطح معنی‌داری شما باشد (مثلاً 0.05)، می‌توانید فرضیه صفر را رد کنید. تفاوت بین میانگین نمونه و مقدار فرضی از نظر آماری معنی‌دار است. نمونه شما شواهد کافی قوی برای نتیجه‌گیری مبنی بر اینکه میانگین جمعیت برابر با مقدار فرضی نیست، ارائه می‌دهد.

یاد بگیرید که چگونه این تحلیل با آزمون Z مقایسه می‌شود.

پیش فرص های آزمون T تک نمونه‌ای

برای نتایج قابل اعتماد آزمون T تک نمونه‌ای، داده‌های شما باید فرضیات زیر را برآورده کنند:

نمونه تصادفی

انتخاب یک نمونه تصادفی از جمعیت هدف شما به شما کمک می‌کند تا اطمینان حاصل کنید که داده‌های شما نمایانگر جمعیت هستند. نمونه‌هایی که آن جمعیت را منعکس نمی‌کنند، معمولاً نتایج نامعتبری تولید می‌کنند.

داده‌های پیوسته

آزمون‌های t تک نمونه‌ای به داده‌های پیوسته نیاز دارند. این متغیرها می‌توانند هر مقدار عددی را بپذیرند و مقیاس را می‌توان به طور معناداری به گام‌های کوچک‌تر تقسیم کرد. به عنوان مثال، دما، قد، وزن و حجم داده‌های پیوسته هستند.

داده‌های توزیع‌شده نرمال یا نمونه شما بیش از ۲۰ مشاهده دارد

این آزمون فرضیه فرض می‌کند که داده‌های شما از توزیع نرمال پیروی می‌کنند. با این حال، وقتی توزیع تک‌وجهی است و اندازه نمونه شما به دلیل قضیه حد مرکزی بیشتر از ۲۰ است، داده‌های شما می‌توانند کمی چولگی (skewness) داشته باشند.

حتماً داده‌های پرت را بررسی کنید زیرا می‌توانند نتایج را تحت تأثیر قرار دهند.

مشاهدات مستقل

آزمون t تک نمونه‌ای فرض می‌کند که مشاهدات مستقل از یکدیگر هستند، به این معنی که مقدار یک مشاهده بر مقدار مشاهده دیگر تأثیر نمی‌گذارد یا به آن وابسته نیست. نقض این فرض می‌تواند منجر به نتایج نادرست شود زیرا این آزمون بر این فرض استوار است که هر نقطه داده اطلاعات منحصر به فرد و جداگانه‌ای ارائه می‌دهد.

چه زمانی از آزمون t تک نمونه‌ای استفاده کنیم?

آزمون t تک نمونه‌ای باید زمانی انتخاب شود که یک نمونه در دسترس باشد و محقق بخواهد مقایسه‌ای بین میانگین مقدار یک متغیر پیوسته در آن نمونه با میانگین مقدار جمعیت (واقعی یا فرضی) انجام دهد. اگر فرضیه مورد نظر این باشد که آیا بین میانگین‌های دو گروه نمونه‌گیری شده تفاوت وجود دارد یا خیر، باید از آزمون t دو نمونه‌ای استفاده شود. علاوه بر این، اگر نمونه‌ها جفت باشند، باید از آزمون t نمونه‌های جفتی استفاده شود.

اگر حجم نمونه کوچک باشد (معمولاً کمتر از ۱۵ به عنوان یک قاعده کلی استفاده می‌شود)، دیگر نمی‌توان فرض کرد که داده‌ها توزیع نرمال دارند و بنابراین باید از یک آزمون ناپارامتری مانند آزمون رتبه علامت‌دار ویلکاکسون تک نمونه‌ای استفاده شود. برای آزمون تفاوت بین میانگین‌ها در بیش از دو نمونه، باید از تحلیل واریانس (ANOVA) استفاده شود.

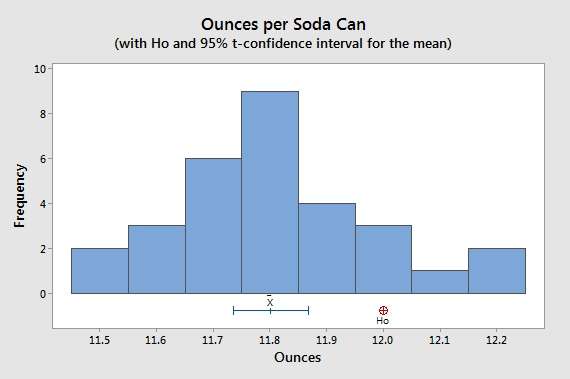
در مثال نوشیدنی، هیستوگرام نشان می‌دهد که داده‌ها چولگی ندارند و هیچ داده پرتی وجود ندارد.

تفسیر نتایج

در اینجا نحوه خواندن و گزارش نتایج آزمون t تک نمونه‌ای آمده است.

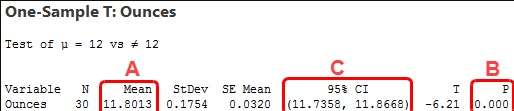
خروجی آماری نشان می‌دهد که میانگین نمونه (A) برابر با ۱۱.۸۰۱۳ است. از آنجا که مقدار p (B) برابر با ۰.۰۰۰ کمتر از سطح معنی‌داری ما یعنی ۰.۰۵ است، نتایج از نظر آماری معنی‌دار هستند. ما فرضیه صفر را رد می‌کنیم و نتیجه می‌گیریم که میانگین جمعیت برابر با ۱۲ اونس نیست. به طور خاص، این مقدار کمتر از مقدار هدف است. شرکت نوشیدنی قوطی‌ها را کمتر از حد لازم پر می‌کند.

بازه اطمینان (C) نشان می‌دهد که میانگین جمعیت برای همه قوطی‌ها احتمالاً بین ۱۱.۷۳۵۸ و ۱۱.۸۶۶۸ اونس است. این محدوده شامل مقدار فرضی ما یعنی ۱۲ اونس نمی‌شود و اهمیت آماری را مجدداً تأیید می‌کند. درباره بازه‌های اطمینان بیشتر بدانید.

مطالب مرتبط مفید

آنالیز واریانس (ANOVA)

فرضیه صفر یا فرض صفر

تحلیل رگرسیون