حداقل مربعات وزنی (WLS)
حداقل مربعات وزنی (WLS) چیست؟
حداقل مربعات وزنی (WLS) نوعی رگرسیون خطی است که هنگام برازش مدل، وزنهای متفاوتی به هر نقطه داده اختصاص میدهد. WLS به جای کمینه کردن مجموع مربعات ساده باقیماندهها، آن طور که حداقل مربعات معمولی (OLS) انجام میدهد، مجموع مربعات وزنی (wi) باقیماندهها را کمینه میکند، همانطور که نماد جمع زیر نشان میدهد:
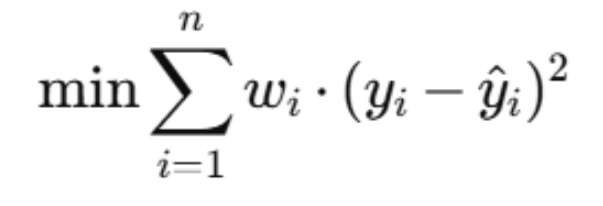
رگرسیون حداقل مربعات معمولی (OLS) روش استاندارد رگرسیون خطی است. این روش به همه نقاط داده وزن یکسانی اختصاص میدهد که معمولاً چیز خوبی است.
با این حال، مواردی وجود دارد که شما نیاز دارید که با استفاده از حداقل مربعات وزنی (WLS) به مشاهدات وزن متفاوتی بدهید. رایجترین دلیل، پرداختن به ناهمسانی واریانس (heteroscedasticity) است که زمانی رخ میدهد که باقیماندهها واریانس ثابتی ندارند. با این حال، چندین مورد مهم دیگر نیز وجود دارد که نیاز به استفاده از WLS دارید. به طور خلاصه، تحلیلگران زمانی از حداقل مربعات وزنی استفاده میکنند که برخورد یکسان با همه مشاهدات، مدل را تحریف کند.
خوشبختانه، رگرسیون حداقل مربعات وزنی از همان مکانیزم رگرسیون معمولی استفاده میکند – عرض از مبدا، ضرایب، آزمونهای t و R-squared همگی به مدل منتقل میشوند. با این حال، تأثیر هر نقطه داده را تنظیم میکند. مشاهدات با دقت یا اهمیت بیشتر، سهم بیشتری در تخمینهای مدل دارند.
در این پست، در مورد شرایطی که حداقل مربعات وزنی میتواند در آنها کمک کند و نحوه انتخاب وزنها بیاموزید.
چه زمانی از حداقل مربعات وزنی استفاده کنیم؟
حداقل مربعات معمولی (OLS) میتواند نتایج غیرقابل اعتمادی ایجاد کند، زمانی که برخی از مشاهدات نویز بیشتری نسبت به سایرین ایجاد میکنند. حداقل مربعات وزنی (WLS) عملکرد مدل را در چندین موقعیت رایج بهبود میبخشد:
- ناهمسانی واریانس: زمانی که واریانس باقیماندهها در سطوح یک پیشبینیکننده تغییر میکند.
- دقت اندازهگیری نابرابر: زمانی که ابزارها برخی از مشاهدات را دقیقتر از سایرین اندازهگیری میکنند.
- نمونهگیری طبقهبندیشده نامتناسب: زمانی که محققان در یک طرح نظرسنجی، زیرگروههای خاصی را بیش از حد یا کمتر از حد نمونهگیری کردهاند.
- آمار نمونه با قابلیت اطمینان متغیر: زمانی که هر نقطه داده خلاصهای (مانند میانگین) با خطای استاندارد خاص خود است.
در هر یک از این موارد، اختصاص وزنهای مناسب به مشاهدات در یک مدل رگرسیون حداقل مربعات وزنی میتواند عدم تعادل را اصلاح کند و منجر به نتایج دقیقتر و قابل اعتمادتری شود.
بیایید این موارد استفاده مختلف را بررسی کنیم!
اصلاح ناهمسانی واریانس (heteroscedasticity)
یکی از رایجترین دلایل استفاده از حداقل مربعات وزنی، اصلاح ناهمسانی واریانس است که زمانی وجود دارد که واریانس باقیماندهها با یک متغیر مستقل افزایش یا کاهش مییابد. در این موارد، تخمینهای حداقل مربعات معمولی (OLS) بدون سوگیری باقی میمانند، اما خطاهای استاندارد، مقادیر p و فواصل اطمینان غیرقابل اعتماد میشوند. حداقل مربعات وزنی با دادن وزن بیشتر به مشاهدات با واریانس باقیمانده کمتر، کارایی را بهبود میبخشد.
اغلب، واریانس باقیمانده غیر ثابت مشکلساز را در نمودارهای باقیمانده برای یک مدل رگرسیون خطی مشاهده خواهید کرد. معمولاً یک شکل بادبزنی مشخص ایجاد میکند، همانطور که در زیر نشان داده شده است:
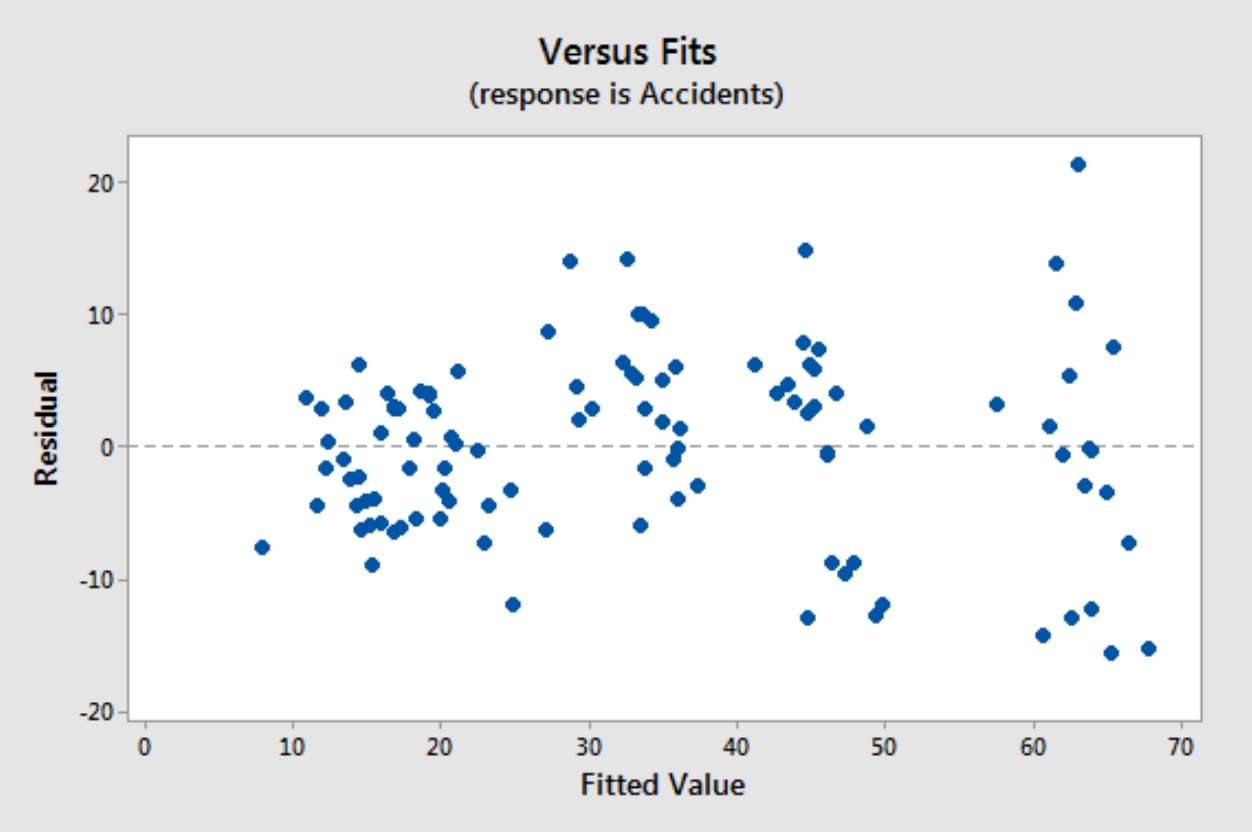
در عمل، ساختار واقعی وزنها معمولاً ناشناخته است، بنابراین باید آن را تخمین بزنیم. این فرآیند اغلب با برازش یک رگرسیون OLS و ارزیابی باقیماندهها آغاز میشود. با این حال، باقیماندههای منفرد برای استفاده مستقیم برای وزندهی بسیار پر سر و صدا هستند. در عوض، ما از باقیمانده مربع برای هر مشاهده به عنوان تخمین تقریبی واریانس خطا در آن نقطه استفاده میکنیم. از طرف دیگر، باقیمانده مطلق میتواند به عنوان تخمینی از انحراف معیار عمل کند، که اغلب در حضور دادههای پرت قویتر است.
در مرحله بعد، ما نحوه تغییر واریانس باقیمانده یا انحراف معیار را در بین مشاهدات، معمولاً به عنوان تابعی از یک یا چند پیشبینیکننده، مدلسازی میکنیم. تابع واریانس یا انحراف معیار حاصل به ما این امکان را میدهد که وزنها را با استفاده از قانون wᵢ = 1 / σ̂ᵢ² برای مدل رگرسیون حداقل مربعات وزنی اختصاص دهیم.
از طرف دیگر، میتوانید از معکوس یک متغیر پیشبینیکننده (به ویژه متغیری که چندین مرتبه بزرگی را در بر میگیرد) به عنوان میانبری استفاده کنید، زمانی که به طور منطقی روند واریانس را تقریب میزند.
وزندهی دقیق
رگرسیون حداقل مربعات وزنی همچنین زمانی مفید است که برخی از اندازهگیریها دقیقتر از بقیه باشند. در دادههای تجربی، محققان ممکن است سطح عدم قطعیت هر اندازهگیری را بدانند.
اگر دقت اندازهگیری هر مشاهده را بدانید، میتوانید آنها را با معکوس واریانس اندازهگیریشان وزندهی کنید و تأثیر بیشتری به مقادیر قابل اعتماد بدهید.
وزنهای طراحی نظرسنجی
روش حداقل مربعات وزنی همچنین هنگام تجزیه و تحلیل دادههای حاصل از نظرسنجیهای پیچیده ارزشمند است. بسیاری از نظرسنجیهای بزرگ از نمونهگیری طبقهبندیشده با انتخاب نامتناسب یا نمونهگیری خوشهای استفاده میکنند که میتواند منجر به احتمالات نابرابر شمول شود. اگر تحلیلگران این ویژگیهای طراحی را در نظر نگیرند، تخمینهای رگرسیون میتوانند مغرضانه یا غیرنماینده باشند.
سازمانهای نظرسنجی اغلب وزنهای نمونهگیری را برای اصلاح این احتمالات نابرابر ارائه میدهند. رگرسیون حداقل مربعات وزنی به شما این امکان را میدهد که این وزنها را مستقیماً در مدل رگرسیون بگنجانید، یکپارچگی طراحی نظرسنجی را حفظ کنید و اطمینان حاصل کنید که نتایج منعکسکننده جمعیت هدف است.
درباره نمونهگیری طبقهبندیشده و نمونهگیری خوشهای بیشتر بدانید.
رگرسیون بر اساس آمارههای نمونه با تغییرات نابرابر
روش حداقل مربعات وزنی همچنین زمانی مفید است که هر مشاهده در مجموعه دادههای شما یک آماره نمونه باشد، مانند میانگین گروه. در این موارد، دقت هر مشاهده بسته به تغییرپذیری داخلی گروه و اندازه نمونه متفاوت است. روش حداقل مربعات معمولی با همه میانگینهای گروه به طور یکسان رفتار میکند، اما روش حداقل مربعات وزنی با دادن وزن بیشتر به میانگینهای دقیقتر، دقت را بهبود میبخشد.
این وضعیت معمولاً در متاآنالیز، رگرسیونهای اکولوژیکی و هر زمینهای که دادهها به جای افراد، گروهها را خلاصه میکنند، رخ میدهد.
اگر هر مشاهده نشاندهنده یک میانگین نمونه باشد، میتوانید وزنها را با استفاده از خطای استاندارد (SE) میانگین محاسبه کنید:
اگر انحراف معیار (SDᵢ) و اندازه نمونه (nᵢ) را برای هر گروه میدانید، خطای استاندارد را محاسبه کنید:
SEᵢ = SDᵢ / √nᵢ
سپس وزن را محاسبه کنید:
wᵢ = 1 / SEᵢ²
برای این وضعیت، حداقل مربعات وزنی از خطای استاندارد میانگین برای وزن به جای انحراف معیار استفاده میکند زیرا خطای استاندارد، دقت میانگین گروه را نشان میدهد. این خطا هم تنوع درون گروه و هم اندازه گروه را در نظر میگیرد و آن را به مبنای مناسبتری برای وزندهی تبدیل میکند.
درباره خطای استاندارد در مقابل انحراف معیار بیشتر بدانید.
مثال
فرض کنید که در حال مدلسازی میانگین نمرات آزمون از مدارس مختلف بر اساس میانگین اندازه کلاس هستید. هر مدرسه میانگین نمره، انحراف معیار و اندازه نمونه خود را ارائه میدهد.
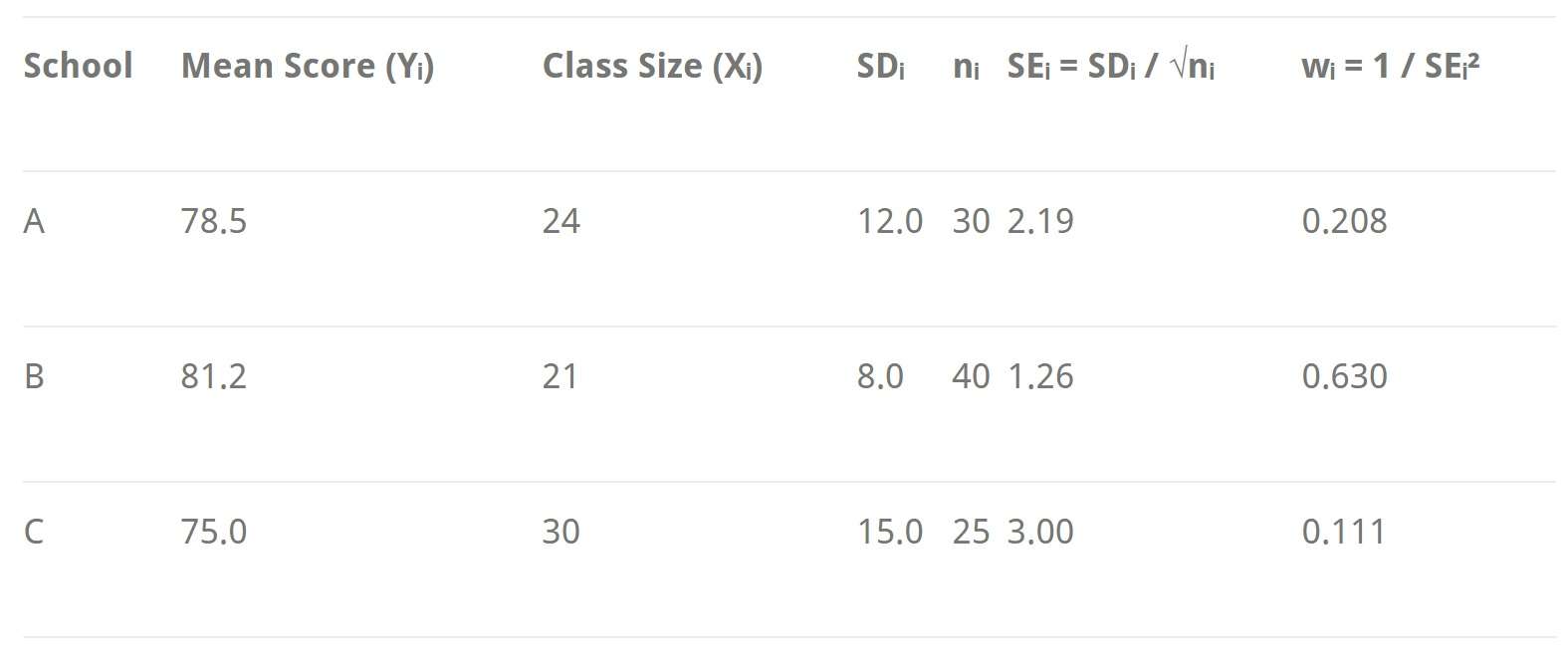
در این مثال:
مدرسه B دقیقترین تخمین (کوچکترین SE) را ارائه میدهد، بنابراین بیشترین وزن را دریافت میکند.
مدرسه C کمترین میانگین دقیق (بزرگترین SE) را دارد، بنابراین سهم کمتری در رگرسیون دارد.
استفاده از این وزنها در یک رگرسیون حداقل مربعات وزنی از میانگین امتیاز بر اندازه کلاس، منجر به مدلی میشود که قابلیت اطمینان متغیر مشاهدات را بهتر منعکس میکند.
مثال حداقل مربعات وزنی
تصور کنید مطالعه شما در حال مدلسازی مصرف برق خانگی (کیلووات ساعت) بر اساس متر مربع است. پس از برازش یک مدل حداقل مربعات معمولی (OLS)، نمودار باقیمانده نشان میدهد که تغییرپذیری با اندازه خانه افزایش مییابد. آمارشناسان به این الگو به عنوان ناهمسانی واریانس اشاره میکنند و این فرض کلیدی OLS یعنی همسانی واریانس را نقض میکند. این میتواند منجر به خطاهای استاندارد غیرقابل اعتماد شود.
برای پرداختن به این موضوع، دادهها را به باندهای اندازه – محدودههایی از متر مربع – تقسیم کنید و واریانس باقیماندهها را در هر باند تخمین بزنید. سپس به هر مشاهده وزنی برابر با معکوس واریانس تخمین زده شده برای باند اندازه آن اختصاص دهید. به عبارت دیگر، خانههای کوچکتر با مصرف برق ثابتتر (واریانس باقیمانده کمتر) وزنهای بالاتری دریافت میکنند.
برازش رگرسیون حداقل مربعات وزنی با استفاده از این وزنها، مدل کارآمدتری را ارائه میدهد. تخمین شیب دقیقتر میشود و فواصل اطمینان و مقادیر p حاصل، نسبت به مدلهای OLS قابل اعتمادتر هستند.





پاسخگوی سوالات و نظرات شما هستیم