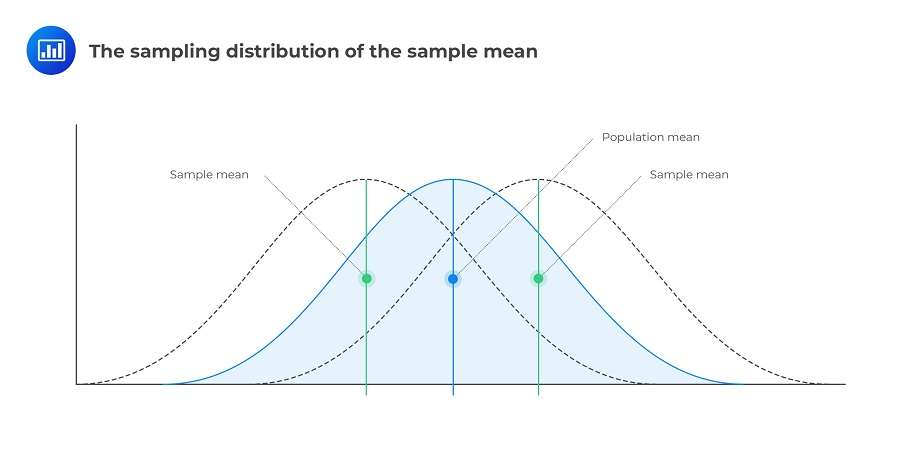
توزیع نمونه گیری (Sampling Distribution)
در آمار، توزیع نمونهگیری، توزیع احتمال یک آماره (مانند میانگین) است که از تمام نمونههای ممکن با اندازه معین از یک جمعیت به دست میآید.
در واقع، توزیع نمونهگیری یک جمعیت معین، توزیع فراوانیهای طیف وسیعی از نتایج مختلف است که ممکن است برای یک آماره از یک جمعیت رخ دهد.
در آمار، توزیع نمونهگیری نشان میدهد که چگونه یک آماره نمونه، مانند میانگین، در نمونههای تصادفی متعدد از یک جمعیت تغییر میکند. این به پیشبینی در مورد کل جمعیت کمک میکند. برای نمونههای بزرگ، قضیه حد مرکزی تضمین میکند که اغلب شبیه توزیع نرمال به نظر میرسد.
هدف از توزیعهای نمونهگیری
آمارهای نمونه فقط پارامترهای جمعیت، مانند میانگین یا انحراف معیار را تخمین میزنند. دلیل این امر این است که در تحقیقات دنیای واقعی، فقط یک نمونه از موارد از جمعیت انتخاب میشود.
به دلیل محدودیتهای زمانی و مسائل عملی، یک محقق نمیتواند کل جمعیت را آزمایش کند. بنابراین، احتمال دارد که میانگین نمونه با میانگین جمعیت (نامشخص) متفاوت باشد.
با این حال، یک محقق هرگز مقدار دقیق خطای نمونهگیری را نخواهد دانست، اما با استفاده از توزیع نمونهگیری، میتواند خطای نمونهگیری را تخمین بزند.
سه توزیع مختلف در ساخت توزیع نمونهگیری دخیل هستند.
- توزیع جمعیت: توزیع تمام مقادیر یا اقلام منفرد در کل جمعیت (N).
- توزیعهای نمونه: توزیع نمونههای تصادفی مختلف گرفته شده از جمعیت (n). در حالی که مفهوم “همه نمونههای ممکن” زیربنای ایده توزیع نمونهگیری است، ما در عمل تعداد نامحدودی را انتخاب نمیکنیم.
- توزیع نمونهگیری: توزیع یک آماره خاص (مانند میانگین) که از هر یک از نمونههای ممکن محاسبه میشود.
نحوه یافتن توزیع نمونهگیری
لازم به ذکر است که توزیعهای نمونهگیری نظری هستند و محقق تعداد نامحدودی از نمونهها را انتخاب نمیکند.
با جمعیت شروع کنید: در حالت ایدهآل، کل جمعیت و پارامترهای آن (N) را بشناسید. با این حال، در بسیاری از موارد، این کار غیرعملی یا غیرممکن است.
اندازه نمونه را انتخاب کنید: اندازه نمونه خود را که با n نشان داده میشود، تعیین کنید.
برای ایجاد توزیع نمونهگیری، تحقیق باید:
- نمونهگیری تصادفی: نمونههای متعددی با اندازه n را به صورت تصادفی از جمعیت انتخاب کنید. این فرآیند بارها تکرار میشود، هر بار یک نمونه جدید انتخاب و میانگین آن محاسبه میشود. توزیع این میانگینهای نمونه، توزیع نمونهگیری میانگین نمونه را تشکیل میدهد.
- محاسبه آماره نمونه: برای هر نمونه، آماره مورد نظر (مثلاً میانگین) را محاسبه کنید.
- تعیین تفاوت: تفاوت بین میانگینهای نمونه را برای هر نمونه انتخاب شده محاسبه کنید. بزرگی تفاوت میتواند تحت تأثیر اندازه نمونه قرار گیرد. نمونههای بزرگتر اغلب تخمینهای قابل اعتمادتر و پایدارتری از میانگین جمعیت ارائه میدهند که منجر به توزیع باریکتری از تفاوتها میشود.
- ساخت توزیع: تفاوتها در میانگینهای نمونه را رسم کنید تا توزیع آنها را تجسم کنید و آمارههای مرتبط (مثلاً میانگین تفاوتها، خطای استاندارد تفاوت) را برای توصیف این توزیع محاسبه کنید.
قضیه حد مرکزی (Central Theorem Theory)
در کاربردهای عملی، رسم نمونههای نامحدود برای ایجاد توزیع نمونهگیری امکانپذیر نیست. با این حال، مفهوم رسم «تمام نمونههای ممکن» یک پایه نظری است که زیربنای ایده توزیع نمونهگیری است.
در عمل، ویژگیهای توزیع نمونهگیری (مانند میانگین و خطای استاندارد آن) اغلب با استفاده از نظریه آماری و دادههای یک نمونه واحد، با کمک اصولی مانند قضیه حد مرکزی، استنباط میشوند.
قضیه حد مرکزی به ما میگوید که صرف نظر از توزیع جمعیت، شکل توزیع نمونهگیری با افزایش اندازه نمونه (N) به نرمال بودن نزدیک میشود.

این قضیه مفید است، زیرا تحقیق هرگز نمیداند کدام میانگین در توزیع نمونهگیری با میانگین جمعیت برابر است، اما با انتخاب نمونههای تصادفی زیاد از یک جمعیت، میانگینهای نمونه با هم خوشهبندی میشوند و به تحقیق اجازه میدهند تخمین بسیار خوبی از میانگین جمعیت داشته باشد.
بنابراین، خطای نمونهگیری با افزایش اندازه نمونه (n) کاهش مییابد.
قضیه حد مرکزی با اطمینان از اینکه توزیع نمونهگیری میانگین نمونه وقتی اندازه نمونه بزرگ است، قابل پیشبینی (توزیع نرمال) میشود، مبنایی برای بسیاری از روشها و استنتاجهای آماری فراهم میکند.



پاسخگوی سوالات و نظرات شما هستیم