میانگین چیست و چطور آن را پیدا کنیم؟
میانگین چیست؟
میانگین در ریاضی و آمار، کل مجموعه دادهها را با یک عدد واحد که نشاندهنده نقطه مرکزی دادهها یا مقدار معمول است، خلاصه میکند. این میانگین همچنین به عنوان میانگین حسابی شناخته میشود و رایجترین معیار گرایش مرکزی است. اغلب به آن “میانگین” میگویند.
انواع مختلفی از میانگین وجود دارد، از جمله میانگین هندسی و هارمونیک. اما در این پست، ما بر میانگین حسابی، رایجترین شکل آن، تمرکز میکنیم.
یاد بگیرید که چگونه میانگین را پیدا کنید و بدانید چه زمانی آماره خوبی برای استفاده است و چه زمانی نیست!
چگونه میانگین را پیدا کنیم؟
یافتن میانگین بسیار ساده است. فقط تمام مقادیر را جمع کنید و بر تعداد مشاهدات تقسیم کنید. فرمول میانگین در زیر آمده است:
X1+X2+…+Xn/n
برای مثال، اگر قد پنج نفر ۴۸، ۵۱، ۵۲، ۵۴ و ۵۶ اینچ باشد، برای یافتن میانگین به این صورت عمل میکنیم:
۴۸ + ۵۱ + ۵۲ + ۵۴ + ۵۶ تقسیم بر 5 = ۵۲.۲
میانگین قد آنها ۵۲.۲ اینچ است.
فرمول میانگین
دو نسخه از فرمول میانگین در ریاضی وجود دارد – فرمولهای نمونه و جامعه. در هر مورد، فرآیند یافتن میانگین از نظر ریاضی تغییر نمیکند. مقادیر را جمع کرده و بر تعداد مقادیر تقسیم کنید. با این حال، نمادگذاری فرمول بین این دو نوع متفاوت است.
فرمول میانگین نمونه
فرمول میانگین نمونه به شرح زیر است:
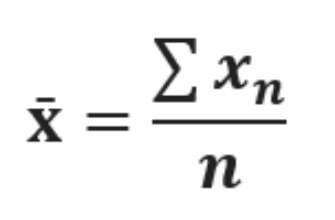
که در آن:
x̄ میانگین نمونه متغیر x است.
∑xn = مجموع n مقدار.
n = تعداد مقادیر موجود در نمونه.
معمولاً، نمادگذاری فرمول نمونه از حروف کوچک استفاده میکند.
فرمول میانگین جمعیت
فرمول میانگین جمعیت به شرح زیر است:
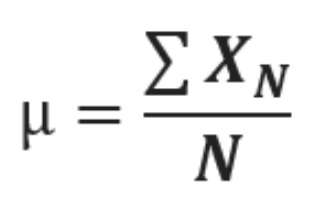
که:
µ میانگین جمعیت است.
∑XN = مجموع N مقدار.
N = تعداد مقادیر در جمعیت.
معمولاً، فرمول میانگین جمعیت از حروف یونانی و بزرگ استفاده میکند.
چه زمانی از میانگین استفاده میکنید؟
در حالت ایدهآل، میانگین در ریاضی (معروف به میانگین) نشاندهندهی ناحیهای است که بیشتر مقادیر در یک توزیع در آن قرار میگیرند. آمارشناسان از آن به عنوان مکان مرکزی یک توزیع یاد میکنند. میتوانید آن را به عنوان تمایل دادهها به خوشهبندی حول یک مقدار میانی در نظر بگیرید. هیستوگرام زیر، میانگین را با دقت نشان میدهد که مرکز توزیع دادهها را پیدا میکند.
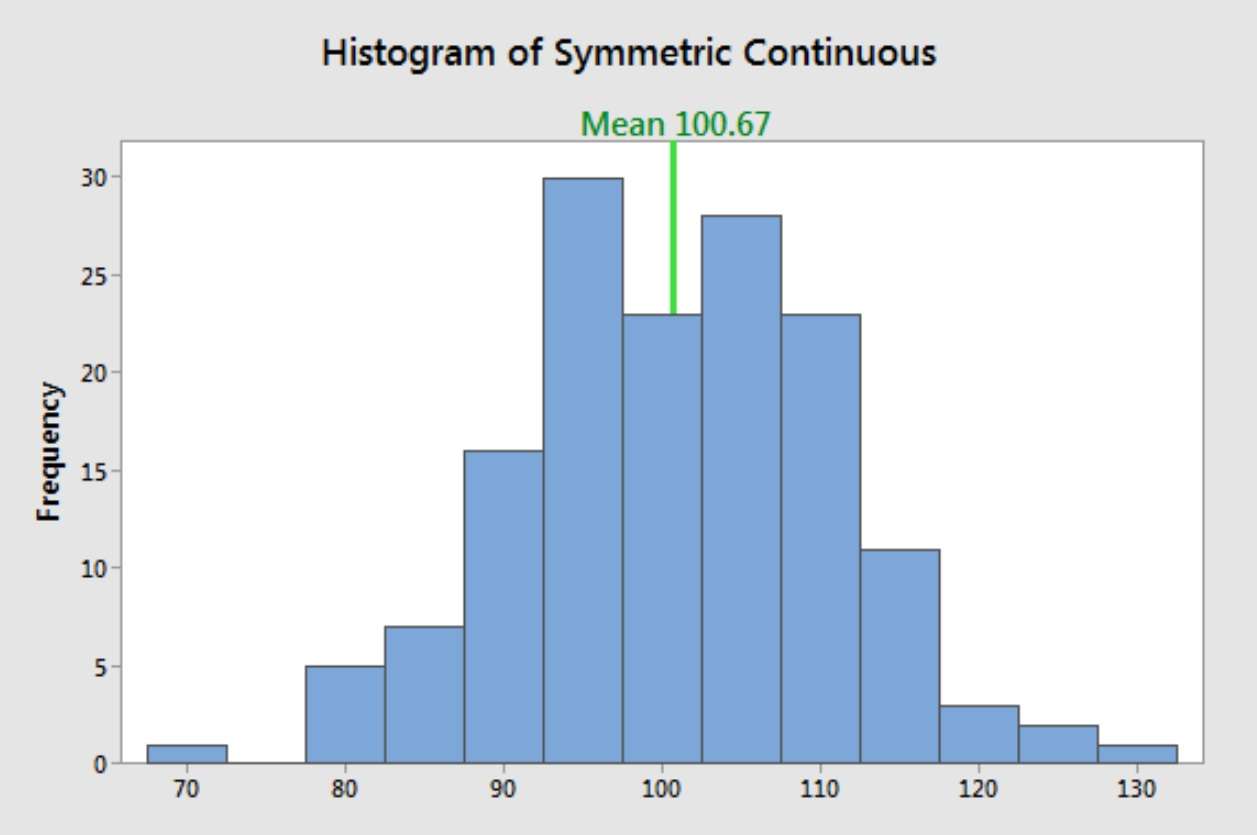
با این حال، میانگین همیشه مرکز دادهها را پیدا نمیکند. این روش به دادههای اریب و مقادیر شدید حساس است. برای مثال، وقتی دادهها اریب هستند، میتواند خطا کند. در هیستوگرام زیر، میانگین خارج از ناحیهای با رایجترین مقادیر قرار دارد.
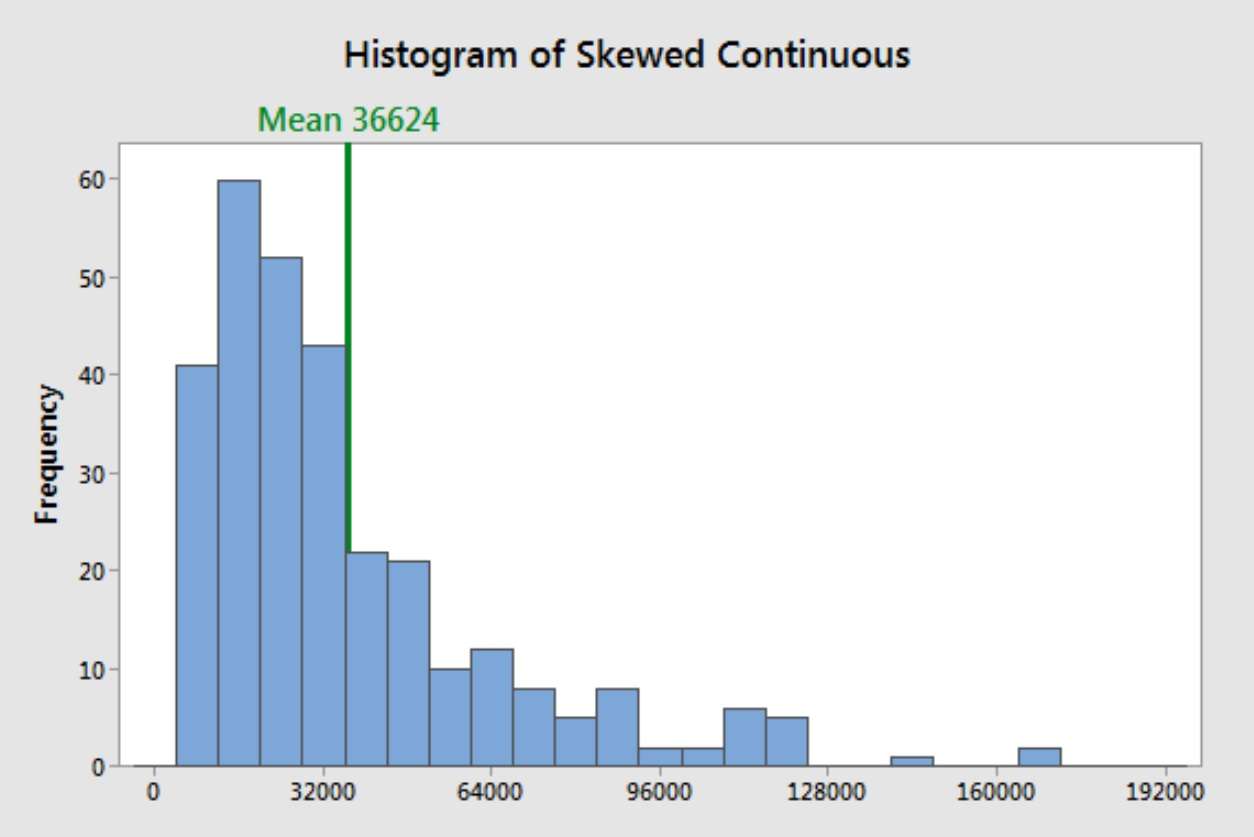
این مشکل به این دلیل رخ میدهد که دادههای پرت تأثیر قابل توجهی بر میانگین دارند. مقادیر شدید در یک دنباله طولانی، آن را از مرکز دور میکنند. هرچه توزیع کجتر میشود، میانگین از مرکز دورتر میشود.
در این موارد، میانگین میتواند گمراهکننده باشد زیرا ممکن است نزدیک به رایجترین مقادیر نباشد. در نتیجه، بهتر است وقتی توزیع متقارنی دارید، از میانگین برای اندازهگیری گرایش مرکزی استفاده کنید.
برای توزیعهای اریب، اغلب بهتر است از میانه یا میانگین اصلاحشده استفاده کنید که از روشهای مختلفی برای یافتن مکان مرکزی استفاده میکنند. توجه داشته باشید که میانگین هیچ اطلاعاتی در مورد تغییرپذیری موجود در یک توزیع ارائه نمیدهد. برای ارزیابی این ویژگی، انحراف معیار را ارزیابی کنید.
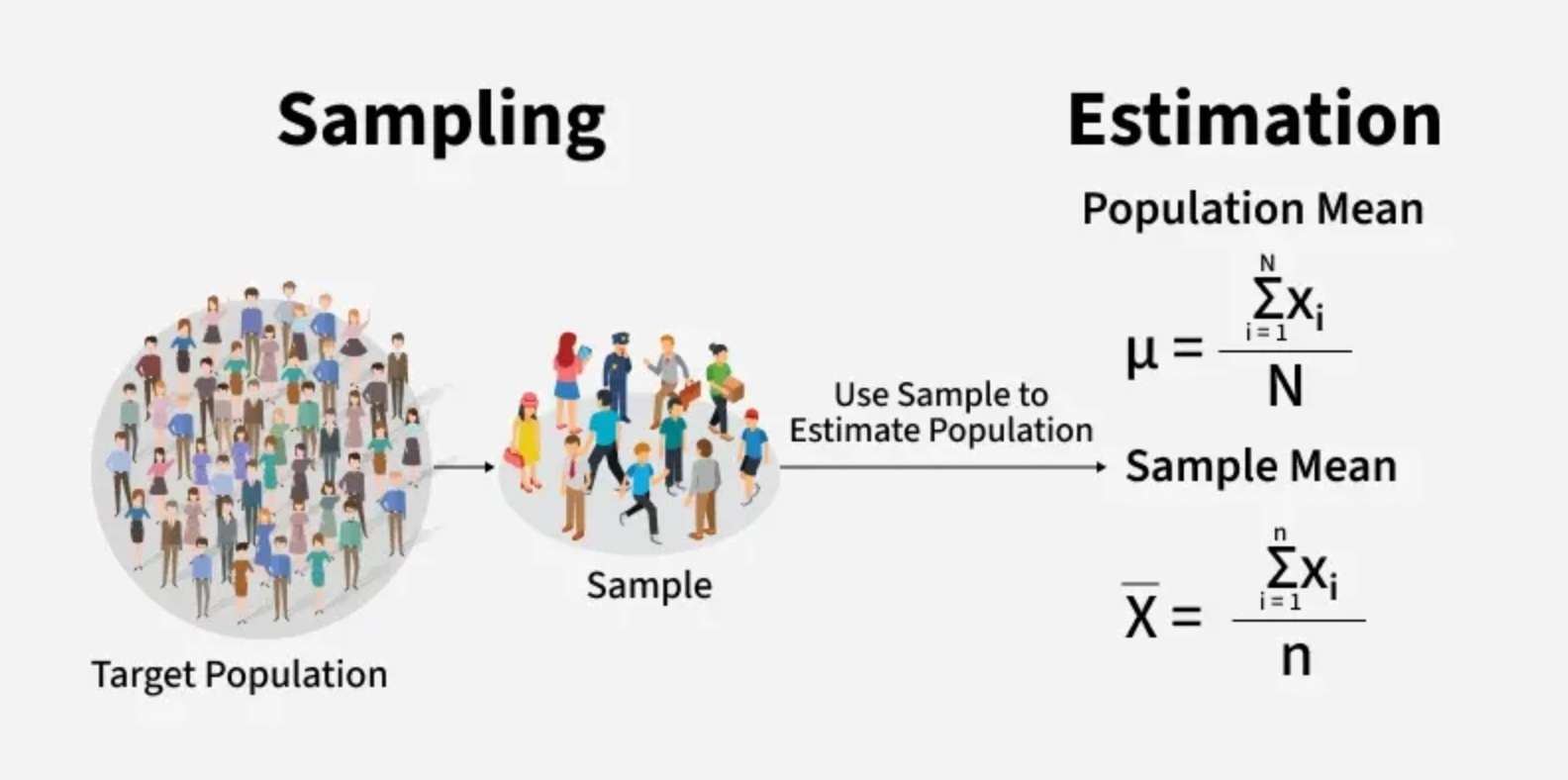
استفاده از میانگینهای نمونه برای تخمین میانگینهای جمعیت
در آمار، تحلیلگران اغلب از میانگین نمونه به عنوان تخمین نقطهای میانگین جمعیت استفاده میکنند. برای نمونههای کوچک، نمونه میتواند تفاوت زیادی با جمعیت داشته باشد. با این حال، با افزایش اندازه نمونه، قانون اعداد بزرگ بیان میکند که میانگین نمونه احتمالاً به مقدار جمعیت نزدیک خواهد بود.
آزمونهای فرضیه، مانند آزمونهای t و ANOVA، از نمونهها برای تعیین اینکه آیا میانگینهای جمعیت متفاوت هستند یا خیر، استفاده میکنند. آمارشناسان به این فرآیند استفاده از نمونهها برای تخمین ویژگیهای کل جمعیتها، آمار استنباطی میگویند.
در آمار، معمولاً از میانگین حسابی استفاده میکنیم، که ما در این پست روی آن تمرکز میکنیم. با این حال، انواع دیگری از میانگینها، از جمله نسخه هندسی، نیز وجود دارند. که بعدا درباره آن مطلبی خواهیم نوشت. همچنین یک میانگین وزنی وجود دارد.
حالا که در مورد میانگین آماری میدانید، در مورد بازگشت به میانگین نیز بیاموزید. یعنی تمایل بازگشت رویدادهای شدید به سمت رویدادهای معمولیتر.



پاسخگوی سوالات و نظرات شما هستیم